- #1
Bassel AbdulSabour
- 8
- 0
I just want to know the difference between those rules:
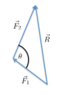
1. R^2 = F1^2 * F2^2 + 2*F1*F2*COS(the angle between F1 and F2)
2. The second is about the parallelogram rule, it says that the two vectors are added and their summation is the magnitude of the resultant.
Which one is correct?
1. R^2 = F1^2 * F2^2 + 2*F1*F2*COS(the angle between F1 and F2)
2. The second is about the parallelogram rule, it says that the two vectors are added and their summation is the magnitude of the resultant.
Which one is correct?