- #1
robertjford80
- 388
- 0
Homework Statement
The Attempt at a Solution
Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5
The numbers in parentheses are, respectively, the usual definition of a Fourier series, and the formulas for the coefficients of the series.If a periodic function f(x) with period ##2\pi## is piecewise continuous in the interval ##-\pi \leq x \leq \pi## and has a left-and right-hand derivative at each point of that interval, then the corresponding Fourier series (7) [with coefficients (6)] is convergent. Its sum is f(x), except at a point x0 at which f(x) is discontinuous and the sum of the series is the average of the left- and right-hand limits of f(x) at x0.
robertjford80 said:
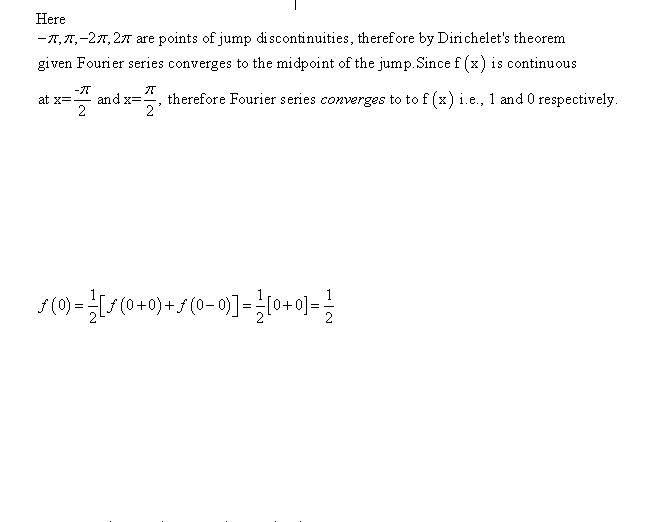
The Attempt at a Solution
Obviously brackets mean something other than parentheses because .5[0 + 0] ≠ .5
A Fourier series convergence is a mathematical concept that describes how a periodic function can be represented as a sum of simple sine and cosine functions. It is used to approximate and analyze functions in fields such as engineering, physics, and signal processing.
The convergence of a Fourier series is determined by evaluating the partial sums of the series and checking if they approach the original function as the number of terms increases. If the partial sums converge to the function, the Fourier series is said to converge.
Fourier series convergence is important because it allows us to approximate complex functions with simpler trigonometric functions, making it easier to analyze and manipulate them. It also has many practical applications in fields such as electrical engineering, acoustics, and image processing.
Some conditions for a Fourier series to converge include the function being represented being periodic, continuous, and piecewise smooth. The function must also have a finite number of discontinuities and the integral of the function over one period must exist.
No, a Fourier series can only converge to a periodic function. If a function is not periodic, its Fourier series will not be able to accurately represent it. However, by extending the function periodically, its Fourier series can still be used to approximate it.