Fourier Series: Exploring Java Applet Questions

[purejoker]

Fourier series ...

Hi, everyone, I’m new to these forums. I’m just doing some work on Fourier analysis, and just have a few curious questions, I just need to clear up, and so I understand it better.

I have been playing around with the java applet for Fourier series from this website:
http://www.falstad.com/fourier/
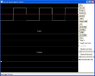
check attachmebt...

My question:

The red line is meant to represent the synthesised signal, if the number of terms is set to zero, the red line is flat. But there is a white dot under cosines, and none at all under sines. Also if you place the cursor over the white dot in the cosines, it shows the magnitude. This also appears as zero.

What I don’t understand is why there is dot in the cosines and none in the sines, if the terms are set to zero shouldn’t they both have no dots? And why does the dot in the cosines have a magnitude zero?

I’m a bit confused about this can some help?

Thanks alots

 

[kbfrob]

the dot under cosines represents the constant term a_0, or a_0cos(0x). the reason that this is zero is because the function is zero. notice that if you raise or lower the dot, the function remains a constant function, with a higher or lower value appropriately.

you can do this for any of the given functions. changing the first cosine term just adds a constant.

 

[purejoker]

the redline is flat because the terms are zero.

the cosine has a dot which is zero which comes from:

a0 = 2/T ∫ x(t) dt

is this right?

 

[kbfrob]

i'm not sure of your bounds of integration, but you have the right idea. the reason it is lumped in with the cosines is because it is really ∫x(t)cos(0x)dt.

 

[purejoker]

if i increase the numbers of terms, the sines get different magnitude values to match the square wave, but all the cosines values are still zero, why is that?

 

[kbfrob]

square wave is an odd function, so its Fourier series will only have sine terms.

 

[purejoker]

x(t) = ½ a0 + Σ an.cos(n.ω.t) + Σ bn.sin(n.ω.t)

this bit basicly always equal zero

Σ an.cos(n.ω.t) = 0 in a square wave.

i get it thanks alot!

 

[kbfrob]

right. you can see this is true because a_n=∫x(t)cos(nωt)dt. x(t) is odd, cos(nωt) is even, so their product is odd and a symmetric integral over an odd function is 0.

thank you too for showing me that applet. excellent way to show Fourier series graphed.