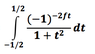- #1
tquiva
- 20
- 0
Homework Statement
I am asked to find the Fourier transform of w(t)=1/(1+t^2)
Homework Equations
I know the only equations I need are:
The Attempt at a Solution
Therefore, I attempted the following:
I tried to expand the function in the integral and got:
I then tried to solve for this integral in terms of t from -1/2 to 1/2, and instead, the calculator says "Non-real result" and doesn't give me an answer. I know that exp(-ift)=cos(ft)+isin(ft) so the equation contains a complex part. But is there something else I need to do that I missed in my process? I even tried entering this integral into MatLab and still get the same answer as my Ti-89. I am now so frustrated.
Can someone please help me? I don't want to do a fft on Matlab or anything. I need to figure out this method. My assignment is due soon, so any help is greatly greatly appreciated. Thank you.