- #1
laurens
- 4
- 0
I try to build a loading diagram in the lateral direction of an aircraft, however have not succeeded yet.
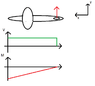
For example, in the z-direction (direction where weights and lift of the aircraft point). I have made a simple loading diagram. I first assumed a simple beam, which is hinged at the wing and the horizontal tail surface. Then adding all the weights to the aircraft, I could balance them when I assumed that the aircraft was flying in a straight and level flight. An example of this can be seen in the attached files.
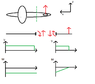
Now this was assumed to be just a static case. However now I want to calculate the loads in lateral direction, for example when a gust hits the vertical fin. In the attached files I put a top-down view of such a load case. In this picture I also drew the shear force and moment, as I though they would act on the aircraft. Since there is no static equilibrium anymore I first assumed I could maybe simplify it as this. However when calculating with "real" values, I got incredibly high stresses at the nose of the aircraft.
So although this is not a static problem, is there any possibility to draw a shear force and moment diagram as I would have done in the static case?
Can I maybe assumed that I cut somewhere in the tail and then assume from the cut to the rear of the fuselage as beam. Which is then clamped at the cut? As an example I drew the third picture. So that in the rest of the fuselage the bending moment is constant? Or is this really not allowed to use as a first estimation of the fuselage loading? If this is not allowed, maybe someone has a suggestion to build such loading diagrams?
For example, in the z-direction (direction where weights and lift of the aircraft point). I have made a simple loading diagram. I first assumed a simple beam, which is hinged at the wing and the horizontal tail surface. Then adding all the weights to the aircraft, I could balance them when I assumed that the aircraft was flying in a straight and level flight. An example of this can be seen in the attached files.
Now this was assumed to be just a static case. However now I want to calculate the loads in lateral direction, for example when a gust hits the vertical fin. In the attached files I put a top-down view of such a load case. In this picture I also drew the shear force and moment, as I though they would act on the aircraft. Since there is no static equilibrium anymore I first assumed I could maybe simplify it as this. However when calculating with "real" values, I got incredibly high stresses at the nose of the aircraft.
So although this is not a static problem, is there any possibility to draw a shear force and moment diagram as I would have done in the static case?
Can I maybe assumed that I cut somewhere in the tail and then assume from the cut to the rear of the fuselage as beam. Which is then clamped at the cut? As an example I drew the third picture. So that in the rest of the fuselage the bending moment is constant? Or is this really not allowed to use as a first estimation of the fuselage loading? If this is not allowed, maybe someone has a suggestion to build such loading diagrams?