- #1
dynamicskillingme
- 27
- 0
Homework Statement
For a gauge function G(t,q) where
does
stevendaryl said:Oh, so you're just talking about Lagrangian mechanics.
If [itex]G[/itex] is a function of [itex]q[/itex] and [itex]t[/itex], then you have:
[itex]\dot{G} = \frac{\partial G}{\partial q} \dot{q} + \frac{\partial G}{\partial t}[/itex]
So in that case, [itex]\frac{\partial \dot{G}}{\partial \dot{q}} = \frac{\partial G}{\partial q}[/itex]
dynamicskillingme said:A quick question about the same function, wouldbe a true statement?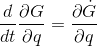
stevendaryl said:Yes, if [itex]G[/itex] is only a function of [itex]q[/itex] and [itex]t[/itex].
dynamicskillingme said:G is a function of q and t, (G(t,q) to be exact). Could you explain why you can change the order of the derivatives in this case?
Gauge transformations are mathematical operations that change the way a physical quantity is measured without changing its physical properties. They are commonly used in fields such as physics, engineering, and mathematics.
G(t,q) represents the gauge transformation function, which is a mathematical function that relates the values of a physical quantity at two different points in space and time. It is used to express the transformation of a physical quantity under a gauge transformation.
Yes, G(t,q) can be expressed differently depending on the specific gauge transformation being applied. Different gauge transformations will have different functional forms for G(t,q), but they will all ultimately relate the values of a physical quantity at two points in space and time.
The purpose of gauge transformations is to simplify the mathematical description of physical systems. By using gauge transformations, we can choose a different way of measuring a physical quantity that may make the equations describing the system simpler and easier to work with.
Gauge transformations have many applications in fields such as electromagnetism, quantum mechanics, and general relativity. They are used to simplify equations, describe physical systems, and understand the underlying symmetries and invariances of a system.