- #1
astrobird
- 22
- 2
I'm reading a book that deals with Gauss's law for electric fields in its differential form. I'm stuck now on a page that discusses taking deriviatives of the equation for a vector field:
→
A
I'm familiar with the rules for deriviatives of products and quotients but unfortunately I cannot follow the steps that are being done in this case.
Would someone here be able to add a bit of extra info to what the page explains? Or refer me to a resource that explains the same principles but with more intermediate steps?
Here is the relevant part of the page which I scanned:
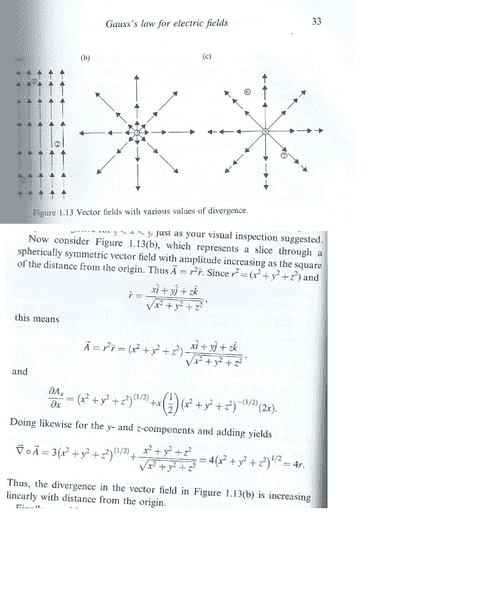
→
A
I'm familiar with the rules for deriviatives of products and quotients but unfortunately I cannot follow the steps that are being done in this case.
Would someone here be able to add a bit of extra info to what the page explains? Or refer me to a resource that explains the same principles but with more intermediate steps?
Here is the relevant part of the page which I scanned: