- #1
GreenLantern674
- 27
- 0
A sphere of radius 2a is made of nonconducting material that has a uniform volume charge density . (Assume that the material does not affect the electric field.) A spherical cavity of radius a is now removed from the sphere, as shown in Figure P19.62. Show that the electric field within the cavity is uniform and is given by Ex = 0 and Ey = a/30. (Hint: The field within the cavity is the superposition of the field due to the original uncut sphere, plus the field due to a sphere the size of the cavity with a uniform negative charge density -.)
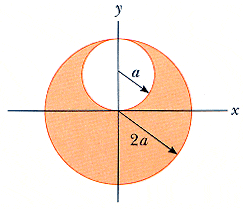
I really don't have any idea how to solve this one. I have a vague idea about ratios of volume to charge. I know it must involve something with that because of the measurement of charge density, but some specifics would really be appreciated.
I really don't have any idea how to solve this one. I have a vague idea about ratios of volume to charge. I know it must involve something with that because of the measurement of charge density, but some specifics would really be appreciated.