- #1
BadSkittles
- 34
- 0
Hello everyone, I am puzzled by how the sum of the tension forces on a rope is calculated.
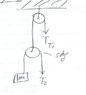
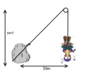
So let's say a climber (5kg) is dangling on a cliff, with a rope around his waist. That same rope is wrapped around a rock (10 kg) 50 meters left of the cliff. How would the tension force of that rope be measured when the rope goes in different directions.
What about a pulley? Is the tension force just the sum of the mass * gravity?
Also, what is the equation for tension forces. Is it just the sum of all forces that the rope is tugged by?
Help is much appreciated
So let's say a climber (5kg) is dangling on a cliff, with a rope around his waist. That same rope is wrapped around a rock (10 kg) 50 meters left of the cliff. How would the tension force of that rope be measured when the rope goes in different directions.
What about a pulley? Is the tension force just the sum of the mass * gravity?
Also, what is the equation for tension forces. Is it just the sum of all forces that the rope is tugged by?
Help is much appreciated