- #1
ngkamsengpeter
- 195
- 0
Please help me to solve the following question :
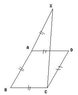
ABCD is a parallelogram .BA is procude to X and BA=AX . Prove that angle of XCB is 90 degree.
ABCD is a parallelogram .BA is procude to X and BA=AX . Prove that angle of XCB is 90 degree.