Geometry construction problem

[Maria_arch]

Hello everybody, i am new to this forum, i am not a physicist not a mathematician, just an architect and i have a geometrical problem that has drove me crazy. I thought to sign in JUST in case someone can help find a solution.

I am working with autocad, that means using geometry consructions all the time. I have many automatic constructions (like circle tangent to 3 elements) but I came across this problem i could NOT construct.

I ll try to describe it the best i can since i don't know the exact term in English

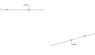
-I have two lines that are not parallel: LineA and LineB
-A specific point pA on lineA
-A specific point pB on lineB

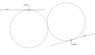
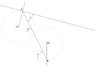
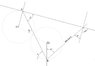
I want to construct two circles (cA) and (cB) that have the same radius and
circleA is tangent to LineA, to circleB and 'passes' from pointA
circleB is tangent to LineB, to circleA and 'passes' from pointB

The final result i want to construct would be like an S connecting the two lines

I don't know if this is a darn toooo easy problem but honestly with my level of knowledge i CAN NOT solve it! As you understand i don't want to solve it algebrically

Thank you very much in advance

PS sorry if this post in in the wrong thread

ps2 i found how to atach image... 1.jpg is the problem, 2.jpg is what i want to construct, 3.jpg is the final result

 

[zgozvrm]

Have you found a solution yet?


I've determined that there are 2 types of situations for non-parallel lines:

1) The line through points A & B is perpendicular to the line which bisects the angle formed by lines A & B

2) The line through points A & B is NOT perpendicular to the line which bisects the angle formed by lines A & B.


Situation #1 is easy.

I'm still working on situation #2

 

[coolul007]

There are 3 line segments.

AO Perpendicular from line A to the center O, of the circle tangent to line A. Length r.
AQ Perpendicular from line B to the center Q, of the circle tangent to Line B. Length r.
OQ from conecting the centers of the two circles tangent. Length 2r.

r is a range dependent on the distance from point A to point B.

More later

 

[Studiot]

Does this sketch help?

RST is the common tangent between the two circles

S and T are intersection points for two tangents to a circle. Therefore the tangents are equal.

That is SA = SR and TR = TB

 

[Maria_arch]

ok, i have been 'playing' a bit with the problem (when ever i feel like i can actually find the solution) just in case i find some properties that can help me and found this... i don't know if it help but it might give you a clue about the solution.

I 've drawn a set of two equal random circles from my points A & B
Found the middle of the... the... arch(?) M1

Then i did the same thing with another set (different radius)
Found point M2

I performed the same with a third set of circles

I found there is a line (M1-2) that passes from all these points. This means (i think) the tangent point i am looking for is on this line

I also found that the angle this line forms with lineA and lineB is half of angleAB
This is certain cause since i am testing them in Autocad i can have a total acuracy in angles and distances.

I am attaching again some images as example

P.S. Thanks for putting your minds on this

 

[Maria_arch]

and forgot to say that the distance from point A to the section point A1 of lineA and lineM12 is the same as from B to the section point B1 of lineB and lineM12

see image again

 

[Studiot]

I am not quite sure what you menat by your last two posts, but my calculations do not put the common tangent point of the two circles on the bisector of angle formed by the intesection of your two straight lines.

Did you make anything of the stuff I posted?

You haven't yet posted quite enough information to solve the problem since you must know both the inclination of the lines and the distance AB and their distances from the intersection point ie their coordinates if you will.

Also what exactly do you mean by no calculation?

 

[coolul007]

I am not quite sure what you menat by your lst two posts, but my calculations do not put the common tangent point of the two circles on the bisector of angle formed by the intesection of your two straight lines.

Did you make anything of the stuff I posted?

You haven't yet posted quite enough information to solve the problem since you must know both the inclination of the lines and the distance AB and their distances from the intersection point ie their coordinates if you will.

Also what exactly do you mean by no calculation?

It seems to me even knowing AB distance and angle, there would still be a range of radii that would work.

 

[Maria_arch]

I am not quite sure what you menat by your last two posts, but my calculations do not put the common tangent point of the two circles on the bisector of angle formed by the intesection of your two straight lines.

Did you make anything of the stuff I posted?

You haven't yet posted quite enough information to solve the problem since you must know both the inclination of the lines and the distance AB and their distances from the intersection point ie their coordinates if you will.

Also what exactly do you mean by no calculation?

Look, first maybe you are totally right, i am just experimenting trying to find properties, i am not ever sure if they are correct, that's why i always ask people more advanced in math.
So in any case its good to know i was wrong. (good opportunity to experiment and find where i was wrong)

As for your sketch, i saw it, i understand it but i can't figure out how i ll find points S&T since i only know A&B and not r?

PS: I must also point out that since i know plain English (I am Greek) and i am not familiar with the technical math terms ( i had to look to a dictionary what 'inclination' is), sketches are much appreciated!
Ah... Greek too :tongue:

 

[Studiot]

First welcome to PF, Maria.

Second

(I am Greek)

That is very good since this is mainly about Euclid, who was a very famous Greek.

My current sketch is too large for the scanner so I will have to make it small enough to post here.

Meanwhile I can tell you that in my first sketch (sorry it is so faint)
$$\theta$$ is the angle subtended by the first arc (it is arc, not arch - that is a bridge) to the centre of its circle.
$$\phi$$ is the angle subtended by the reverse arc in the second circle

My first sketch is not large enough to show the intersection (crossing) point of the two lines but I have called the angle between them $$\alpha$$.

It can be shown that $$\alpha$$ = $$\phi$$ - $$\theta$$

There are some other formulae to do with the shapes, but I will leave posting these until the next sketch to make them clear.

 

[Maria_arch]

Yes, maybe that's why i like geometry (very usefull in my work) and maybe that's why this is driving me CRAAAAAZY...

I just like geometry and i like searching for logical problems solutions... consider it a hobbby
The last problem i was searching was how to construct a circle tangent to a line and passing through 2 point
I know, after hours of reading i discovered Apollinius problem and got the solution (more hours of reading)
I also learned in the process how to geometrically construct the square root of a distance!
My colleagues and boss say that i have psychological math problems but anyway...

Ok back to your sketch... CD is the line i am searching for, and ST is a line a can not construct yet there for i don't know either the angles Φ or Θ
Also i can't find angle α in the sketch

I undestand that TR is 'mirror' of TB (axis TC) and the same happens with SR-AC

pffff i like stupid in cases like these!

 

[Studiot]

OK here is a solution using trigonometry.

Please note that this is a different drawing from my previous one, so I have called the angles by new names to avoid confusion.

You do know the following

Where A and B are so you know the distance AB and the direction of the line AB
The direction of the line through A
The direction of the line through B

You can therefore calculate the angle between line AB and line A as the difference of these directions. I have called this angle alpha.
You can therefore calculate the angle between line AB and line B as the difference of these directions. I have called this angle gamma.

You need to know the radius of the circles , which you do not yet know.

To do this first calculate the auxiliary angle I have called beta, which is the difference in the directions of the the line joining the circle centres and the line AB.

Since you do not yet know where the centres are you must calculate this angle as shown in the attachment.

Once you have this angle you can use it to calculate the radius, again as shown in the attachment.

In principle if you can calculate it you can draw it, but I have yet to figure out a drawing construction to replace this.

For your further information, it is also possible to calculate reverse curves when there are two diffeent radii involved.

go well

 

[Maria_arch]

ah... mind food!
yes, i see your sketch and understand it (it took me a while)
Thanks so much for dealing whith this, although i am also looking for the drawing construction i am right now 'prossesing' your solution and experimenting a little bit...

 

[Maria_arch]

I found this, i don't know if its correct but it seems like it might be

I know angle alpha and gamma, looking for beta (sketch1)

If i construct a help line from point B using angle alpha it seems like i found angle beta (sketch2)

I haven't proven it, its just experimenting but if its true then i might be able to drawing construct the line i want that connects the two centers C1 & C2
(i don't know how exactly i ll do that but anyway)

 

[Maria_arch]

Nop, i did some testings and i think my last post doesn't apply to all cases

 

[Studiot]

Sorry to disappoint you but I'm not convinced that your angle is beta.
See my attachment.

Edit there is an arithmetic error in the last line I need to change.

Ok it's correct now. Sorry.

 

[zgozvrm]

OK here is a solution using trigonometry.

Please note that this is a different drawing from my previous one, so I have called the angles by new names to avoid confusion.

You do know the following

Where A and B are so you know the distance AB and the direction of the line AB
The direction of the line through A
The direction of the line through B

You can therefore calculate the angle between line AB and line A as the difference of these directions. I have called this angle alpha.
You can therefore calculate the angle between line AB and line B as the difference of these directions. I have called this angle gamma.

You need to know the radius of the circles , which you do not yet know.

To do this first calculate the auxiliary angle I have called beta, which is the difference in the directions of the the line joining the circle centres and the line AB.

Since you do not yet know where the centres are you must calculate this angle as shown in the attachment.

Once you have this angle you can use it to calculate the radius, again as shown in the attachment.

In principle if you can calculate it you can draw it, but I have yet to figure out a drawing construction to replace this.

For your further information, it is also possible to calculate reverse curves when there are two diffeent radii involved.

go well

Your work is completely correct. However, it is not a "solution."

According to the OP, they are only given the 2 lines and the respective tangent points, A & B. The goal is to determine what the radius of the circles needs to be in order for them to not only be tangent to their respective lines, but tangent to each other, as well.

In other words,:
Given two non-parallel lines and a point on each line, we need to construct an s-curve consisting of 2 arcs having the same radius, such that the distance between the centers of those arcs is twice that radius.

Your "solution" assumes you already have the circles and lines, but don't know the radius of the circles.

 

[Studiot]

Your work is completely correct. However, it is not a "solution."

I'm sorry I don't follow your objection, or for that matter your solution.

The problem is a bog standard one in surveying for railway, mining and road engineering as is the solution I offered.

 

[zgozvrm]

I'm sorry I don't follow your objection, or for that matter your solution.

The problem is a bog standard one in surveying for railway, mining and road engineering as is the solution I offered.

First of all, I never gave a solution. I'm actually still looking for one.


Secondly, I misstated why I feel you didn't give an adequate solution:
The OP is looking for a geometric solution that doesn't involve calculations that are subject to rounding errors. (Think straightedge and compass). For example, it is easy to construct the bisector of an angle using only those tools. Granted, we could also measure the angle with a protractor, divide that measurement in half and draw in the bisector by measuring this new angle with the protractor, but this method is much less accurate (even in AutoCAD).

 

[Studiot]

The OP is looking for a geometric solution

No I think Maria was working in a drawing office and looking for a draughting solution, which is quite different.

I also stated that I didn't have any sort of drawn solution only a calculated one, which I though was better than none.

I would, however be interested in a drawing solutuin since it must be possible to draw what can be calculated. I am just not a first class draughtsman (or even second class really).

So please post if you come up with anything.

If it helps I can let you have the surveyors screed on the subject.

 

[coolul007]

This problem seems so easy on the surface but difficult in practice. I have started an approach to the problem by solving it with constructions if the lines were parallel. Of course I know they are not. I will post my approach in hopes of it sparking someone else while I continue working on it.

 

[coolul007]

Here is a solution, it is not a solution with both circles tangent to each other, but they intersect in equal arcs with equal radii. This seems to me to be adequate for any construction job. All of the following steps correspond to the attached drawing:
1) Draw line segment AB
2) Draw perpendicular from point A
3) Draw perpendicular from point B
4) Extend line A
5) Extend line B
6) The measure of angle CAB = a
7) The measure of angle ABD = a-θ
8) Compute angle from AC and BD to be equal solve: a-x = a-θ+x, x = θ/2
9) Add θ/2 to angle DBA, subtract θ/2 from CAB
10) Draw the new angle line segments to intersect at point F, This forms isosceles triangle AFB.
11) Bisect segments BF and AF
12) Draw perpendiculars from the midpoints of the segments to intersect BD and AC
13) Points H and J are the center of the two circles that are tangent to line A and line B
14) The circles are not tangent to each other but intersect at a point to create equal arcs

Yes, the above requires some cleanup and formalization, however, you get the point.

 

[zgozvrm]

I have discovered and proven the following, which reveals one point that lies on the line tangent to both circles (also know as the perpendicular bisector of the line segment connecting the circles' centers). I can do this using ONLY drafting techniques. The problem is, I haven't found a way to locate a 2nd point on that line.

But, it's a start; maybe it will help.

Here are the steps:
1) extend lines A and B so that they intersect at point P
2) draw the angle bisector of angle APB
3) draw perpendicular bisector of line segment AB
4) the intersection of these 2 lines lies on the common tangent line to the 2 circles

If we can find a 2nd point on that line, then we can find the common tangent (obviously), which means we can find the angle of the line connecting the circles' centers. Using this information, I would be able to solve the problem.

 

[coolul007]

I have discovered and proven the following, which reveals one point that lies on the line tangent to both circles (also know as the perpendicular bisector of the line segment connecting the circles' centers). I can do this using ONLY drafting techniques. The problem is, I haven't found a way to locate a 2nd point on that line.

But, it's a start; maybe it will help.

Here are the steps:
1) extend lines A and B so that they intersect at point P
2) draw the angle bisector of angle APB
3) draw perpendicular bisector of line segment AB
4) the intersection of these 2 lines lies on the common tangent line to the 2 circles

If we can find a 2nd point on that line, then we can find the common tangent (obviously), which means we can find the angle of the line connecting the circles' centers. Using this information, I would be able to solve the problem.

What is the proof that the intersection lies on the tangent line.

I think that the radii have a minimum and maximum that can make this true. That is why this becomes such a difficult problem, as 3 simultaneous events must occur.

 

[zgozvrm]

Here is the proof (albeit, not a completely formal one):

To show this is true, I start with 2 circles and the tangent lines which intersect at point P.
As per the problem requirements, the circles have the same radius and intersect at only one point.

A couple of definitions:
- Let the distance from a point to a line be defined as the length of the segment drawn from the point perpendicularly to the line.
- Any point lying on the bisector of an angle is equidistant from each ray of the angle
- Any point lying on the perpendicular bisector of a line segment is equidistant to each of the segment’s endpoints.

Line AP is tangent to the upper circle (circle C) at point A.
Likewise, line BP is tangent to the lower circle (circle D) at point B.

- Draw the line segment AB
- Draw the perpendicular bisector of segment AB

- Draw the line segment CD
- Draw the perpendicular bisector of CD. This line is tangent to both circles
- Label the intersection of the 2 bisectors as point E

Now, all I have to do is show that point E lies on the angle bisector of angle APB.

- Draw segment EF perpendicular to AP with point F on AP
- Draw segment EG perpendicular to BP with point G on BP
(for clarity, since I have located point E, I will remove segment AB, circles C and D, and the perpendicular bisectors from the drawing)

So, if I can show that EF = EG then I’ve shown that it lies on the bisector of angle APB.

- Draw segments AC and BD
- We know that AC = BD since they represent the radius of the circles
- We know that AC is perpendicular to AP and BD is perpendicular to BP (since AP is tangent to circle C and BP is tangent to circle D)

- Draw segments EA and EB
- Since E lies on the perpendicular bisector of AB, then EA = EB

-Draw segments EC and ED
- Since E lies on the perpendicular bisector of CD, then EC = ED
- Therefore, by SSS, we know that triangle ACE = triangle BDE

- EF is parallel to AC since both are perpendicular to AP
- EG is parallel to BD since both are perpendicular to BP
- Angle AEF = angle CAE by alternate interior angles
- Angle BEG = angle DBE by alternate interior angles
- Angle CAE = angle DBE by congruent triangles
- Therefore, angle AEF = angle BEG by transitivity

- Angle EFA = angle EGB = 90 degrees, by definition of perpendicular
- Triangle AEF = triangle BEG by AAS
- Therefore EF = EG by congruent triangles

 

[coolul007]

Thanx

 

[coolul007]

BTW, Point E lies on the circumscribed circle of triangle ABP, for what that's worth.

 

[zgozvrm]

That may be helpful! What's the proof for that?

 

[coolul007]

Referring to your diagram above:
AB is a chord of the circumscribed circle for triangle ABP
A perpendicular bisector of a chord AB, bisects the arc at E
angle P is an inscribed angle, intercepting the arc AB
The bisector for angle P, bisects the intercepted arc AB at its midpoint E

 

[verty]

Here is another proof for coolul007's claim.

In the quad AEBP:

A = EBG -- (congruent triangles)
EBG + B = 180 degrees -- (angles on a straight line)
A+B = 180
E+P = 360 - (A+B) = 180
AEBP is a cyclic quad -- (opposite angles form straight angles).

 

[Physs]

Im a 2nd year student and really really confusing for us this things...

 

[Studiot]

Hello physs and welcome to Physics Forums.

Perhaps if you were to explain your difficulty someone could help.

Did you really want to post in this old thread?

 

[micromass]

Please start a new thread if you have a question.