Geometry of a conformal disk

[JoshSmith]

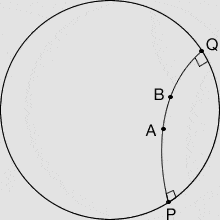
For better or worse, I've begun to work Penrose's book Road to Reality. In the second chapter, one of his exercises (supposedly simple) has entirely eluded me. Penrose presents the conformal Poincaré disk and gives the equation for hyperbolic distance between two points $$A$$ and $$B$$ inside the circle: $$\log\frac{QA\cdot PB}{QB\cdot PA},$$ where $$P$$ and $$Q$$ are the points where the Euclidean circle through $$A$$ and $$B$$ orthogonal to the bounding circle meets the bounding circle and where $$QA, QB, PA, PB,$$ are Euclidean distances. See the figure below.

Now, Penrose simply says that you can include the $$C$$ of Lambert's area formula, which is given by the equation $$\pi-(\alpha+\beta+\gamma)=C\Delta$$ (where $$\Delta$$ is the area of the triangle and $$C$$ is some constant), by multiplying the distance formula above by $$C^{-1/2}$$, where $$C\neq 1$$. He asks if you can see a simple reason why.

My feeling is that it's because $$AB$$ is just one side of a triangle, and $$C$$ must be adjusted thereby. But this feels incomplete at best, and entirely off-track at worst. Any ideas? A hint in the right direction would be better than the outright correct answer. Thanks in advance!

 

[jvicens]

Hello there,

I can understand your confusion with this exercise. The reason why you need to include the C of Lambert's area formula is because the conformal Poincaré disk is a non-Euclidean geometry and therefore the usual Euclidean distance formula does not apply. In this geometry, the distance between two points is given by the logarithm of the ratio of the Euclidean distances, as you have correctly stated.

However, when we introduce the C of Lambert's area formula, we are essentially adjusting for the curvature of the space. The constant C represents the curvature of the space and is not equal to 1 in this non-Euclidean geometry. Therefore, we need to include it in the distance formula to account for this curvature.

To understand this better, think of it this way: In Euclidean geometry, the sum of the angles in a triangle is always equal to 180 degrees. However, in non-Euclidean geometries like the conformal Poincaré disk, this is not the case. The sum of the angles in a triangle will be less than or greater than 180 degrees, depending on the curvature of the space. This is where the constant C comes into play.

I hope this helps to clarify the concept for you. Keep up the good work with Penrose's book and don't hesitate to ask for further clarification if needed.