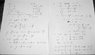Geometry Problem (triangles)

[asura]

Homework Statement

ABC is an equilateral triangle with sides of 2 cm. BC is extended its own length to point D and point E is the midpoint of AB. ED meets AC at F. Find the area of quadrilateral BEFC in square centimeters in simplest radical form. Show all work and clearly label figure(s).

Homework Equations

pythagorean theorem?

The Attempt at a Solution

I could solve for the area of BEFC by making AF = 2-x and FC = x, but it's really convoluted and messy. Is there a simpler way of finding BEFC?

 

[misho]

Yeah, the Pythagorean theorem definitely comes up.

I suggest the following:

1. assign some coordinate axes to your problem. I think B(0,0) and C(2,0) would be good.
2. find the coordinates of all the points (except F, F is the hard one). The coordinates of E are 1/2 those of A (that should be fairly straightforward).
3. find the equation of line DE
4. find the equation of line AC
5. find the coordinates of F by find the intersection of the above two lines
6. use the y-coordinate of E to find the area of triangle BED
7. use the y-coordinate of F to find the area of triangle CFD
8. subtract the above two areas to find the needed area

I'm not sure if I'm supposed to do this (I guess someone will scold me if I'm not), but I attached a picture of how I solved the problem. It's a little messy (it's what I was writing while I was thinking about your problem), but should be readable.

 

[tron_2.0]

i did the problem and got the same thing as misho.

 

[Tedjn]

misho is correct, but there is an easier way to do it without using messy coordinates if you know a few geometric properties.

I would first suggest drawing AD, because then we have another triangle to work with. In particular, you should notice something special about the new triangle ABD from the lengths of its sides and its angles.

There is a fact in geometry that says the three medians of the triangle divide a triangle into 6 smaller triangles of equal area. What line can you draw in ABD that would make this fact useful?

There, you've solved it

Note: Consequently, you should be able to find x/(2-x) very easily. What is point F to triangle ABD?

 

[misho]

That's really neat. I didn't know about that theorem. Weird that in 6 or more years of geometry, it's never come up. It's a fairly easy one to prove, too. Then again, here in Ontario, they didn't even teach us that medians cut each other in a 2 to 1 ratio, and that little fact has come in useful in a number of courses I've taken.

 

[Tedjn]

I'm not surprised it didn't. In the US, too, we don't learn and we don't teach geometry well. Unfortunately, a lot of it has to come from self-study.