- #1
Rectifier
Gold Member
- 313
- 4
The problem
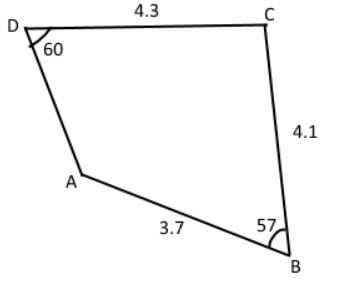
a) find the length of AD in the figure
b) Why are there two solutions in a) and what solution fits the figure?
Figure
The attempt
I started with drawing a "help line" in the figure.
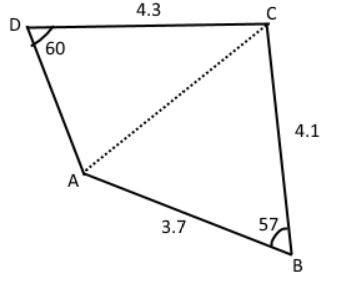
The cosine formula for AC with respect to triangles ADC and CBA gives us two equations:
## AC^2 = 4.1^2 + 3.7^2 - 2 \cdot 3.7 \cdot 4.1 \cdot cos(57) ##
and
## AC^2 = 4.3^2 + x^2 - 2 \cdot 4.3 \cdot x \cdot cos(60) ##
Setting these two equal to each other gives a polynomial of the 2nd degree that has two roots ## x_1=2.47886 ## and ## x_2=1.82114 ##. (These solutions are correct)
I am stuck at b). I have no idea how to continue.
a) find the length of AD in the figure
b) Why are there two solutions in a) and what solution fits the figure?
Figure
The attempt
I started with drawing a "help line" in the figure.
The cosine formula for AC with respect to triangles ADC and CBA gives us two equations:
## AC^2 = 4.1^2 + 3.7^2 - 2 \cdot 3.7 \cdot 4.1 \cdot cos(57) ##
and
## AC^2 = 4.3^2 + x^2 - 2 \cdot 4.3 \cdot x \cdot cos(60) ##
Setting these two equal to each other gives a polynomial of the 2nd degree that has two roots ## x_1=2.47886 ## and ## x_2=1.82114 ##. (These solutions are correct)
I am stuck at b). I have no idea how to continue.
Last edited: