- #1
jasonchiang97
- 72
- 2
1. Homework Statement
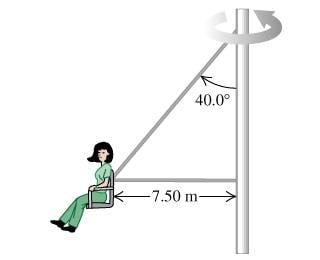
In one of the versions of the "Giant Swing", the seat is connected to two cables, one of which is horizontal (Figure 1) . The seat swings in a horizontal circle at a rate of 33.0 rev/min .
If the seat weighs 295 N and a 869-N person is sitting in it, find the tension in the horizontal cable.
Fc=mv2/r
Period=circumference/velocity so 2πR/v
I drew two FBD(free body diagrams). One for the person and one for the chair
For the person : TsinΘ-W-Fn=0
T=(W+Fn)/sinΘ
Fn = Weight of the chair
For the chair: Th+TcosΘ=mv2/r
Th = mv2/r - TcosΘ
mv2/r - [(Wc + Wp)/sinΘ]*cosΘ
To get the velocity, we use period = circumference /velocity
33 rev/min * 1min/60 sec = 0.55 rev/sec
0.55 = 2π(7.5)/v
v=85.68m/s
m= (Wp + Wc)/9.8
So (Wp+Wc/9.8)(81.68)2/7.5 - (295+869)/tan40
Basically I end up getting a huge number and I'm fairly certain that it's wrong but can't see why
In one of the versions of the "Giant Swing", the seat is connected to two cables, one of which is horizontal (Figure 1) . The seat swings in a horizontal circle at a rate of 33.0 rev/min .
If the seat weighs 295 N and a 869-N person is sitting in it, find the tension in the horizontal cable.
Homework Equations
Fc=mv2/r
Period=circumference/velocity so 2πR/v
The Attempt at a Solution
I drew two FBD(free body diagrams). One for the person and one for the chair
For the person : TsinΘ-W-Fn=0
T=(W+Fn)/sinΘ
Fn = Weight of the chair
For the chair: Th+TcosΘ=mv2/r
Th = mv2/r - TcosΘ
mv2/r - [(Wc + Wp)/sinΘ]*cosΘ
To get the velocity, we use period = circumference /velocity
33 rev/min * 1min/60 sec = 0.55 rev/sec
0.55 = 2π(7.5)/v
v=85.68m/s
m= (Wp + Wc)/9.8
So (Wp+Wc/9.8)(81.68)2/7.5 - (295+869)/tan40
Basically I end up getting a huge number and I'm fairly certain that it's wrong but can't see why