- #1
adjacent
Gold Member
- 1,552
- 63
Homework Statement
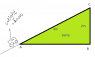
A ramp is shown in the picture.Which ramp is easier to rise an object of mass 2kg up?and why?
Homework Equations
W=FS
The Attempt at a Solution
The second ramp.The work done in rising the mass against gravity is same in the two ramps.That is
W=200N*1 = 200J
But rising in the second ramp,the mass has to move more distance.
200J=5*F So less force is needed F=40N
The first ramp
200J=2*F F=100N
In the second ramp one has to use less force to move it up so it is easier.
My question is:If he uses 40N against gravity(200N),Why doesn't the mass accelerate down?