- #1
FritoTaco
- 132
- 23
Homework Statement
Problem: [itex]y=2-sin\dfrac{2\pi x}{3}[/itex]
Homework Equations
Standard Equation: [itex] y = A sin(B(x - C)) + D [/itex]
- A: amplitude is A
- B: period is [itex]\dfrac{2\pi}{|b|}[/itex]
- C: phase shift is [itex]\dfrac{C}{B}[/itex]
- D: vertical shift is D
The Attempt at a Solution
First, rearrange the equation: [itex]y=-sin\dfrac{2\pi x}{3}+2[/itex]
Amplitude: [itex]1[/itex] (a-value)
Period: [itex]\dfrac{2\pi}{2\pi/3}=\dfrac{2\pi}{1}\cdot\dfrac{3}{2\pi}=\dfrac{6\pi}{2}=3\pi[/itex]
Phase Shift: [itex]0[/itex] (no c-value)
Vertical Shift: [itex]2[/itex] (d-value)
Table (I don't know how to make):
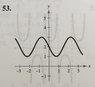
See my attachment for the table of values.
How did I pick my x-values to calculate my y-values?
I used count formula: [itex]\dfrac{1}{4}\cdot \dfrac{3\pi}{1}=\dfrac{3\pi}{4}[/itex]
So, I start from the phase shift and continue adding [itex]\dfrac{3\pi}{4}[/itex] : [itex]0+\dfrac{3\pi}{4}=\dfrac{3\pi}{4}[/itex]
[itex]\dfrac{3\pi}{4}+\dfrac{3\pi}{4}=\dfrac{6\pi}{4}=\dfrac{3\pi}{2}[/itex]
[itex]\dfrac{3\pi}{2}+\dfrac{3\pi}{4}=\dfrac{6\pi}{4}+\dfrac{3\pi}{4}=\dfrac{9\pi}{4}[/itex]
[itex]\dfrac{9\pi}{4}+\dfrac{3\pi}{4}=\dfrac{12\pi}{4}=3\pi[/itex]
I don't want to graph it yet because my table of values doesn't seem correct, in my book the answer is in my second attachment. They don't even use pi for their x-values :(