Green's Function and Variation of Parameters

[member 428835]

Hi PF!

Given operator $B$ defined as $$ B[u(s)] = c u(s) - u''(s) - \frac{1}{2 s_0}\int_{-s_0}^{s_0}(c u(s) - u''(s))\, ds$$ I'm trying to find it's inverse operator $B^{-1}$. The journal I'm reading states $B^{-1}$ is an integral operator $$B^{-1}(u(s)) = \int_{-s_0}^{s_0}G(s,z)u(s)\,ds$$ whose kernal is the Green's function of $B(u)=f : \pm u'(\pm s_0)+c \cot(\alpha) u(\pm s_0) = 0$. The paper I'm reading applies variation of parameters to conclude that

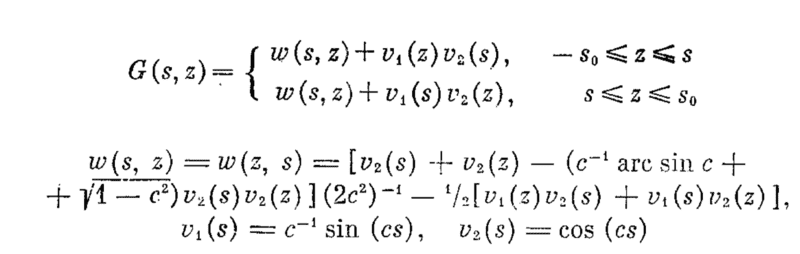
where evidently $v_1$ and $v_2$ solve $$cv(s)-v''(s) = 0;\\
v_1(0)=0,\,v_1'(0) = 1;\\
v_2(0)=1,\,v_1'(0) = 0.$$
Any idea how they determined the $w$ function? I've looked everywhere but can't find a link. I should possibly state that $c = \cos \alpha$ where $\alpha$ is constant.

 

[jvicens]

Hello!

To find the inverse operator $B^{-1}$, we can use the method of variation of parameters. This method involves finding two linearly independent solutions to the homogeneous equation $$cv(s)-v''(s) = 0.$$ These solutions are $v_1$ and $v_2$, with initial conditions as stated in the forum post.

Then, we can define the function $w(s)$ as $$w(s) = \frac{1}{cv_1(s)v_2'(s) - cv_2(s)v_1'(s)}.$$ This function is important because it helps us express the solution to the inhomogeneous equation as an integral involving the Green's function.

To see how this works, we can start with the equation $$B[u(s)] = f(s),$$ and use the variation of parameters method to find the solution as $$u(s) = w(s)\int_{-s_0}^{s_0}G(s,z)f(z)\,dz.$$ Substituting this into the original equation, we can see that it satisfies the equation if the Green's function is defined as $$G(s,z) = \frac{v_1(s)v_2(z) - v_2(s)v_1(z)}{cv_1(s)v_2'(s) - cv_2(s)v_1'(s)}.$$ Therefore, the inverse operator $B^{-1}$ can be written as an integral operator with the Green's function as its kernel.

I hope this helps clarify how the $w$ function is determined and how it relates to the inverse operator. Let me know if you have any further questions.