- #1
tiredryan
- 51
- 0
Hey,
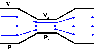
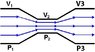
Here's something that confuses me with the Hagen–Poiseuille equation and the Bernoulli's equation. From the Hagen–Poiseuille equation and in general, fluid will tend to flow from high to low pressure. From Bernoulli's equation pressure is a function of cross-sectional area and velocity. So for the figure attached I would expect P1 to be high pressure, P2 to be low pressure so fluid would flow from the high to low pressure. This makes sense.
At P2 the pressure is low, but the pressure increases in the region after P2, let's call it P3. Then how does fluid from from P2 to P3 if the pressure goes from low to high again?
Thanks.
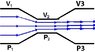
Here's something that confuses me with the Hagen–Poiseuille equation and the Bernoulli's equation. From the Hagen–Poiseuille equation and in general, fluid will tend to flow from high to low pressure. From Bernoulli's equation pressure is a function of cross-sectional area and velocity. So for the figure attached I would expect P1 to be high pressure, P2 to be low pressure so fluid would flow from the high to low pressure. This makes sense.
At P2 the pressure is low, but the pressure increases in the region after P2, let's call it P3. Then how does fluid from from P2 to P3 if the pressure goes from low to high again?
Thanks.