Hard Quantum Mechanics Question

[flydream19]

1. All given variables and known data
Consider a particle of mass m subject to the infinite square well potential function (with L>0)

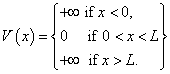
Suppose that you do not know the state function describing the system, but that you are told the expectation value of the position of the particle is given by

$$\left\langle x \right\rangle \left( t \right) = \frac{L}{2} + \alpha L\sin \left( {\Omega t} \right)$$

where α is some unknown constant less than 1/2, and Ω is some frequency greater than zero.

Homework Equations

Equations used in Quantum Mechanics​

Questions:

a. There are many possible values of Ω - what are the allowed values of Ω? (That is, provide an equation for ℏΩ (h-bar*Ω) ). Explain your answer.

b. Write down the most general wave function consistent with this expectation value. Explain your answer.​

 

[strangerep]

So... where is your "attempt at a solution"??

OK, I'll give you a hint: write down the Schrodinger equation applicable to this situation.
Then solve it.

 

[vanhees71]

Where is this question from? I find it quite strange, to say it friendly.

If you look for the state of a system with restricted information like in this example, the best you can do is to look for a statistical operator with maximum (von Neumann) entropy consistent with the given information. This is at least the way to look at this problem from the point of view of Shannon-Jaynes information theory.

 

[Jilang]

This a great question! I've just spent a lovely hour in the sunshine having a go at it. As it is not a stationary state you need at least two terms in the general solution. As you need to arrive at at an expectation value of x that has a sinΩt dependency it looks like you need just two terms. I got that hΩ will represent the difference between the two energy levels of the two terms.

 

[Oxvillian]

Where is this question from? I find it quite strange, to say it friendly.

If you look for the state of a system with restricted information like in this example, the best you can do is to look for a statistical operator with maximum (von Neumann) entropy consistent with the given information. This is at least the way to look at this problem from the point of view of Shannon-Jaynes information theory.

Surely it's just a question about pure states.

This a great question! I've just spent a lovely hour in the sunshine having a go at it. As it is not a stationary state you need at least two terms in the general solution. As you need to arrive at at an expectation value of x that has a sinΩt dependency it looks like you need just two terms. I got that hΩ will represent the difference between the two energy levels of the two terms.

I agree! Perhaps we should add that when you have a superposition of two energy eigenstates, the system will "ring" at the characteristic frequency $\Omega$, as a result of "quantum mechanical cross terms". When you couple the system to an electromagnetic field, it might throw out a photon of that frequency.

 

[strangerep]

Meanwhile, the OP has still made zero attempt at a solution...

 

[unscientific]

Meanwhile, the OP has still made zero attempt at a solution...

What's frustrating is that others who put in decent effort get no replies at all...