How Do You Calculate Amplitude and Time Period in SHM Problems?

[Saitama]

Homework Statement

Question 1)
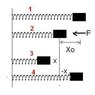
In the figure below, k=100 N/m, M=1 kg and F=10N. A sharp blow by some external agent imparts the speed of 2 m/s to the block towards left. Find the amplitude of the resulting simple harmonic motion.

Question 2)
The string and the spring shown in the figure below are light . The pulley has a moment of Inertia I about its CoM axis and the string does not slip over it. Find the time period of mass m.

Homework Equations

The Attempt at a Solution

For the first Question 1, i used the energy conservation to solve the problem.
Firstly, i found the initial compression in the spring and then formulated the equation as:-
$$\frac{1}{2}Mv^2+\frac{1}{2}kx_o^2=Fx+\frac{1}{2}k(x+x_o)^2$$

x_o=Initial compression in the spring
v=velocity imparted to the block
x=Distance which the block covers after the velocity is imparted (This will be the amplitude)

Now when i plug in the values, i don't get the answer stated in answer key. I don't understand where i am going wrong.

For Question 2), my teacher helped me to formulate the equation.
We take mass m down by a distance of x and then formulate the equation for total energy.
$$E=-mgx+\frac{1}{2}k(x+x_0)^2+\frac{1}{2}mv^2+\frac{1}{2}I(\frac{v}{r})^2$$

In SHM, dE/dt=0 but that's the next step, i have a problem in the equation above.
Why we use a negative sign before mgx? The displacement x and the force mg are in the same direction so why the negative sign appears?

 

[technician]

I don't think that you need to know the value of the force F to find the amplitude of the oscillation.
Do you know how to calculate angular frequency from the information you have been given?
Do you know an expression for maximum velocity in SHM

 

[Saitama]

I don't think that you need to know the value of the force F to find the amplitude of the oscillation.
Do you know how to calculate angular frequency from the information you have been given?
Do you know an expression for maximum velocity in SHM

Yes, i can find out the angular frequency from the given information.
Here,
$$T=2π\sqrt{\frac{m}{k}}$$
Substituting the values, i get T=pi/5 sec.
Since, angular frequency,ω=(2pi)/T, therefore ω=10 rad/sec.
XD I've got it how to do this now. Now, v_max=Aω and v_max=2 m/s, A=0.2m.
Thanks for the help but can you still tell me where i was wrong in my equation?
Also can you help me in the second problem?

 

[Saitama]

Bump. -_-

 

[Saitama]

Umm..i guess no one in the community wants to help me out. =_=

 

[ehild]

The Attempt at a Solution

For the first Question 1, i used the energy conservation to solve the problem.
Firstly, i found the initial compression in the spring and then formulated the equation as:-
$$\frac{1}{2}Mv^2+\frac{1}{2}kx_o^2=Fx+\frac{1}{2}k(x+x_o)^2$$

x_o=Initial compression in the spring
v=velocity imparted to the block
x=Distance which the block covers after the velocity is imparted (This will be the amplitude)Now when i plug in the values, i don't get the answer stated in answer key. I don't understand where i am going wrong.

X is not the amplitude: At the position the external force stops acting the block has both kinetic and potential energy.
The external force did work on the block-spring system: it increased the initial energy. How did you get the initial compression of the spring? ehild

 

[Saitama]

X is not the amplitude: At the position the external force stops acting the block has both kinetic and potential energy.
The external force did work on the block-spring system: it increased the initial energy. How did you get the initial compression of the spring? ehild

Thank you for the reply ehild!

I found the initial compression by the following equation:-
$$F=kx_o$$

So do you mean that the term "Fx" should be added on the left side of the equation?

x is not the amplitude? I am applying law of conservation of energy at the equilibrium position and the extreme position.

 

[ehild]

What do you mean on "initial"? Before the blow or after?
What is F at all? It is not mentioned in the text of the problem. Is it the force of the "sharp blow" or some constant force that compressed the spring before anything else happened and keeps it compressed?

ehild

 

[Saitama]

What do you mean on "initial"? Before the blow or after?
What is F at all? It is not mentioned in the text of the problem. Is it the force of the "sharp blow" or some constant force that compressed the spring before anything else happened and keeps it compressed?

ehild

Sorry for not being clear enough ehild.

By initial, i mean before the blow. "F" is given in the question as 10N. I have used this "F" to find the compression before anything else has happened.

By the way, this is not the exact question. It is a sub question and i got stuck at finding the amplitude. If you wish to check the complete question, you could check the question in the image below:-

 

[ehild]

Hi Pranav,

Thank you for showing the whole problem. It is quite clear now!

I am sure you could answer questions a,b,c.

The sudden blow means that a very high force acts for such a very short time so that the displacement of the block is negligible during the action. The block stays at the equilibrium position, xo=0.1 m while gains speed. It is only approximation. You could determine the change of position if the force have been given.
The problem with that constant force is identical with the situation when a body hangs on a spring. Because of gravity, the spring stretches by xo=mg/kl and oscillation will occur around that equilibrium position. If Δx=x-xo, Δx=Asin(ωt) and ω is the same as for the unstretched spring, ω=sqrt(k/m).

Energy is conserved for the oscillatory motion: 1/2mv^2+1/2k(Δx)^2=constant, but not for the total energy of the spring and kinetic energy of the body: There is the external force F that does work on the body during its oscillation.

ehild

 

[Saitama]

Hi Pranav,

Thank you for showing the whole problem. It is quite clear now!

I am sure you could answer questions a,b,c.

Yes, i can solve the first three parts. :)

Energy is conserved for the oscillatory motion: 1/2mv^2+1/2k(Δx)^2=constant, but not for the total energy of the spring and kinetic energy of the body: There is the external force F that does work on the body during its oscillation.

ehild

So where am i getting wrong in my equation?
Should i form the equation like this:-
$$\frac{1}{2}k{(x+x_o)}^2=\frac{1}{2}Mv^2+\frac{1}{2}kx_o^2+Fx$$

x=distance covered by the block after the blow.
Using the above equation, i get my answer to be 0.2m which matches with the answer in my book. But i am confused that why x is the amplitude here or am i going somewhere wrong with my concepts? A diagram can explain me better on how this block will perform SHM.

Thanks for the help!

 

[ehild]

Nothing is wrong with the new equation, but it differs from the original one. It means: the total elastic energy when the block stops moving is equal to the energy just after the blow (kinetic + elastic) plus the work of the external force along the distance x.
Remember that F=kx₀. If you substitute it into the equation you get 1/2 mv^2=1/2kx^2, the same relation that holds between maximum velocity and maximum displacement of an ordinary SHM.

When there is a constant (compressive) force exerted on the mass on spring the length of the spring changes as L(t)=Lo-xo-Asin(wt). It means an SHM around the new equilibrium length Lo-xo.

In the figure, 1 shows the original length of the spring. 2 is the spring, compressed by the constant force F. 3 is the state of maximum compression after the blow, 4 is the minimum compression. The block oscillates between these positions with amplitude x.

I will try to make you a moving gif picture tomorrow.

The best thing is to do an experiment. If you do not have a spring, a piece of elastic thread will do. Fasten a key or some other object at the end of the thread and let it hang. The thread stretches, it becomes longer then the original length, because of the constant force, gravity. Push the object: it starts oscillating up and down. Observe the maximum and minimum positions: the middle is at the stretched length.

ehild

 

[Saitama]

Remember that F=kx₀. If you substitute it into the equation you get 1/2 mv^2=1/2kx^2, the same relation that holds between maximum velocity and maximum displacement of an ordinary SHM.

Yes, when i substitute F=kx_o, i get the equation 1/2 mv^2=1/2kx^2. So does that mean if i would have used this equation, i would have got the answer?

In the figure, 1 shows the original length of the spring. 2 is the spring, compressed by the constant force F. 3 is the state of maximum compression after the blow, 4 is the minimum compression. The block oscillates between these positions with amplitude x.

Thank you for that image, i understand better now. I was confusing with the mean position, thanks for the clarification. :)

I will try to make you a moving gif picture tomorrow.

ehild

That's very kind of you, sir!

 

[ehild]

Yes, when i substitute F=kx_o, i get the equation 1/2 mv^2=1/2kx^2. So does that mean if i would have used this equation, i would have got the answer?

As you got Xo from kXo=F, the two equations are equivalent. The solutions are the same.

Thank you for that image, i understand better now. I was confusing with the mean position, thanks for the clarification. :)

I am pleased that you understand it better now. You will understand even better when doing an experiment. And it would be quite clear by solving the equation of motion by Calculus.

ehild

 

[Saitama]

Sorry for a late reply!

As you got Xo from kXo=F, the two equations are equivalent. The solutions are the same.

Thanks for clarifying that. :)

I am pleased that you understand it better now. You will understand even better when doing an experiment. And it would be quite clear by solving the equation of motion by Calculus.

ehild

Are you referring to the three equations of motion?
If so, i have already solved them with calculus.

Thank you again! :)

 

[ehild]

Are you referring to the three equations of motion?
If so, i have already solved them with calculus.

I mean Newton's law

$ma=-kx+F$

which means the differential equation $m\frac{d^2x}{dt^2}+kx=F$, with the initial condition x(0)=F/k and x'=V₀.

The general solution is of the form x(t)=Asin(ωt+θ)+F/k, with ω=√(k/m).
Applying the initial conditions,
x(0)=F/k, so θ=0;
x'(0)=v₀ → Aω=₀, A=V₀/ω.

The block moves according to the function $x(t)=\frac{V_0}{\omega} \sin(\omega t)+F/k$ between the turning points

x_max=F/k+V₀/ω and x_min=F/k-V₀/ω.

ehild

 

[Saitama]

I mean Newton's law

$ma=-kx+F$

which means the differential equation $m\frac{d^2x}{dt^2}+kx=F$, with the initial condition x(0)=F/k and x'=V₀.

The general solution is of the form x(t)=Asin(ωt+θ)+F/k, with ω=√(k/m).
Applying the initial conditions,
x(0)=F/k, so θ=0;
x'(0)=v₀ → Aω=₀, A=V₀/ω.

The block moves according to the function $x(t)=\frac{V_0}{\omega} \sin(\omega t)+F/k$ between the turning points

x_max=F/k+V₀/ω and x_min=F/k-V₀/ω.

ehild

Sorry for interpreting your statement wrong.
Thanks for the descriptive explanation. I have never tried that way of solving the SHM questions but it may get useful as i get my practice on it.