- #1
cloud809
- 3
- 0
1. Ideal gas cycle - diesel engine cycle. You begin at some volume V1. Perform an adiabatic compression to V2. Perform an expansion to V3 at constant pressure. Next, perform an adiabatic expansion to V4, Last, it moves back to V1 at a fixed volume, while decreasing temperature back to original starting point.
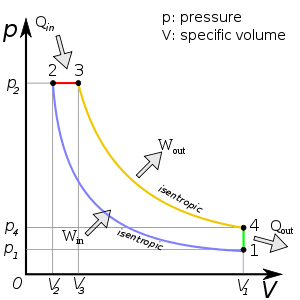
NOTE: Ignore "specific volume," and just consider it to be generic "volume" for my case.
Find Qin and Qout in terms of V1, V2, V3, and T1.
--
2. 1st law: ΔU = W + Q, where W = -∫PdV
We're told that the 1st law is the assumed starting point for this problem.
--
3. For Qin, I began that ΔU = 0 for 2→3, so -W2→3=Qin. This yielded
Qin=- (-∫23PdV)
or Qin = P(V3-V2).
Am I right to assume that ΔU=0 for this 2→3 phase? I can't find how to incorporate V1 and T1 if my method was ok.
--
Then, for Qout, I noted that W = 0 for 4→1, so ΔU4→1=Qout.
So, I found that ΔU = Nk(f/2)BΔT, or Qout = NkB(f/2)(T1-T4). And again, I'm running into the same issue of not filling the parameters of the original question.
NOTE: Ignore "specific volume," and just consider it to be generic "volume" for my case.
Find Qin and Qout in terms of V1, V2, V3, and T1.
--
2. 1st law: ΔU = W + Q, where W = -∫PdV
We're told that the 1st law is the assumed starting point for this problem.
--
3. For Qin, I began that ΔU = 0 for 2→3, so -W2→3=Qin. This yielded
Qin=- (-∫23PdV)
or Qin = P(V3-V2).
Am I right to assume that ΔU=0 for this 2→3 phase? I can't find how to incorporate V1 and T1 if my method was ok.
--
Then, for Qout, I noted that W = 0 for 4→1, so ΔU4→1=Qout.
So, I found that ΔU = Nk(f/2)BΔT, or Qout = NkB(f/2)(T1-T4). And again, I'm running into the same issue of not filling the parameters of the original question.