- #1
neik
- 15
- 0
http://img.photobucket.com/albums/v64/neik7/asg.jpg
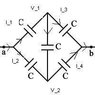
this is neither a parallel nor a series circuit
i duno how to find the equivalent capacitance from a to b
can anyone give me some hint ?
thanks in advance
this is neither a parallel nor a series circuit
i duno how to find the equivalent capacitance from a to b
can anyone give me some hint ?

thanks in advance
Last edited: