- #1
Saladsamurai
- 3,020
- 7
***First part solved skip to post #11
^^^^^^^^^^^^^^^^^^^^^^^^^^^It's a silly title, but I really need help. The four pink balls surround the purple one and all make contact.
Calling the radius of the purple ball r and the radii of the pink R:
Show that r/R=.225.
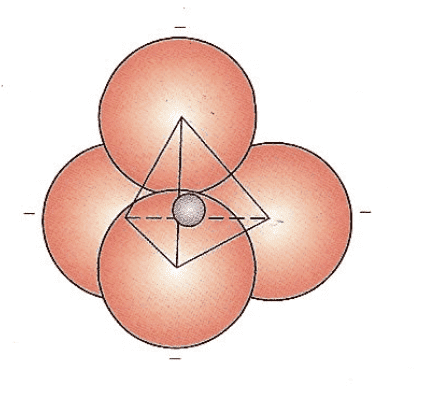
edit: I hijacked this image to simplify the problem. The original problem statement had no image and came from a Materials Science text: "Show that the minimum cation-to-anion ratio for a coordination number 4 is .225"
^^^^^^^^^^^^^^^^^^^^^^^^^^^It's a silly title, but I really need help. The four pink balls surround the purple one and all make contact.
Calling the radius of the purple ball r and the radii of the pink R:
Show that r/R=.225.
The Attempt at a Solution
I think that this can be done with simple plane trig, but I am having troubles with the visualization.Anybody have any ideas? I am dying here.edit: I hijacked this image to simplify the problem. The original problem statement had no image and came from a Materials Science text: "Show that the minimum cation-to-anion ratio for a coordination number 4 is .225"
Last edited: