Force: Help with Dilemma of Containers and Water Mass!

[Azeri]

HELP with Force!

I've got a "dilemma" here about Force:
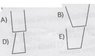
" Containers with different volumes but with the same areas at the bottom are filled with water of equal mass. Will the Force applied to the bottom of containers vary according to container?"

First of all I guess Force must be equal to the Weight [W] of water which is same for all containers W=mg=F , but on the other hand if I calculate it from pressure F=PxA=dghA=dgV (P-pressure,A-area at the bottom, d-density of liquid , V-volume of container) and it varies due to the volume of container.

Thanks...

 

[dextercioby]

The second part of the reasoning is wrong...Tell me why...

Daniel.

 

[Azeri]

The weight of water must cause a pressure . Is that false?

 

[dextercioby]

Of course not,it's the interpretation of "V" that is wrong...

Daniel.

 

[Azeri]

The volume of container V=hxA Supposing it is sylindrical

 

[dextercioby]

Prismatoid...But it's not the volume of the container... It's the volume of the fluid (i.e.water) which is the same for both containers,regardless of which is bigger...

Daniel.

P.S.Ergo,the force is "mg"...

 

[Azeri]

Thanks. But i still can't get how hxA=const if heigts are different? F=PxA=dxgxhxA

 

[dextercioby]

The masses of water are the same.Ergo the volumes are the same.The containers have identical base area.Ergo the water has the same height in both containers.

Daniel.

 

[Azeri]

But he containers have different shapes. One is wide another is narrow.

 

[dextercioby]

WHAT?"but with the same areas at the bottom".Sounds familiar??Your very own hands wrote it in the first post...

Daniel.

 

[Azeri]

Same area but not same shape. one gets wider from the bottom but another is narrow

 

[dextercioby]

How do you know that?Was that specified in your problem?U said "sylinder" (sic),now u make it some weird shape...??

Daniel;

 

[dextercioby]

Can't u make a link,or something??Post it on
www.imageshack.com And then insert the link in the message...

Daniel.

PS.you should have said that in the first place...

 

[Townsend]

Same area but not same shape. one gets wider from the bottom but another is narrow

Are you saying that the bottoms are not flat?

 

[dextercioby]

I thought this problem was going to be simple,but he insists it's more than what i thought previously...

Anyway,let's hope he can come up with a drawing...

Daniel.

 

[Azeri]

tried to attach

 

[dextercioby]

And the question is the same??Pressure force acting on the base??It's the hydrostatic pressure times the area of the base.The hydrostatic pressure is the product between the water density,the "g" acceleration and the height of the water column.

In which case the height of the colum is greatest...??

Daniel.

 

[Azeri]

The height is greatest in narrow one(D) but what about F=W=mg ? that's the point where i am confused.

 

[Doc Al]

I thought we answered this same problem here:
https://www.physicsforums.com/showthread.php?t=60468

(Please do not double post!)

 

[Azeri]

In that post you answered about pressure. I need help with force applied

 

[FulhamFan3]

if they're both the same mass than the force will be the same. It's the pressure that could be different. P=dgh is only dependent on height. The water itself will always take up the same amount of volume if the mass is equal. If the vase narrows towards the top that means more water will have to be stored higher up. Hence more pressure. If it widens out like a bowl that means it will be more shallow and the height will be lower.

 

[Azeri]

Then you mean that calculating F=PxA is not usefull here

 

[FulhamFan3]

Just use F=mg

 

[Gokul43201]

The error in the second line of reasoning is that the hydrostatic pressure at the bottom of the liquid is assumed to be all that contributes to a vertical force on the container. This is not true. The vertical component of the forces (due to hydrostatic pressure along the walls) on all the sloping walls will be transferred to the bottom. In a stright cylinder, the forces on the walls have no vertical component (the normal reaction is horizontal), so the hydrostatic pressure on the base contributes entirely to the force.
F = P*A = Ahdg = Vdg = mg.

In any case with outward sloping walls, F = PA(bottom) + vertical component of $\int_0^H P(h)dA(h)$ on walls.
So, F > PA(bottom).

With inward sloping walls the normal reaction has a vertical component that actually points upwards.
So, F = PA(bottom) - vertical component of $\int_0^H P(h)dA(h)$ on walls.

Does this clarify things, or should I solve a specific example ?