How Do I Correctly Insert My Population Growth Model Syntax in Mathematica?

[mardusj]

Hey everyone,
I am struggling to properly insert my simple model syntax in mathematica for a population growth.

The formula is as following:
Rate of growth over time = birth rate*N - death rate*N + net migration rate*N

I have been trying to add saturation to the model for the population N.

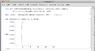
That's my syntax attached only with the birth Rate included. The graph I am getting is somewhat weird.

sol1 = NDSolve[{D[x[t],t]==r x[t] (1-x[t]/k), x[0]==100} /. {r->1.4, k-> 100000},x[t], {t,0,100}]Plot[x[t] /. sol1, {t,0, 100}]N/K is the saturation.

Also, sometimes with the same syntax inserted, there's an error popping up, see attachment 2.

thanks in advance for any help.

 

[Bill Simpson]

The error in your attachment 2 appears to be because you have rx[t] instead of r x[t] or r*x[t], that little space is critically important.

In your Plot I include PlotRange->All so that the default range selection doesn't only display what it believes is the "interesting stuff."

Now can you be more concrete about what problem you are having? "The graph I am getting is somewhat wierd" is too abstract for me to determine what to look at.

 

[mardusj]

Thank you Bill!

Basically I am trying to make a simplistic prediction of a population growth of Germany in the next couple of years. In the attachment you can see the values r, d, and m. R is rate of birth, D is death rate, and M is migration rate. 82 here is the current population of germany in millions, and K is the maximum carrying capacity so to say, or the saturation built in the model in order not to have an exponential growth. My aim is to show in this graph that the line should have a decreasing trend. I am currently having troubles with the correct scaling. The X-axis is supposed to be time in years. Any ideas on how to better do it?

And again thanks for your help so far

 

[Bill Simpson]

If I rearrange your equation just a bit then I think I get

D[x[t], t] == (r - d + m)*x[t]/(1 - x[t]/k)

That seems to me to say that r,d,m don't interact with each other in any way or indepenedntly interact with x[t] and could all be combined into a single constant.

If your model is only describing the net external flux of population with that then that might be fine.

You have the current population (82) implying millions, but you don't say whether the r,d,m also implying millions. r=d+m==-2060 so does that mean there are 2060 million leaving each year? That would certainly explain why this.

Table[{t, x[t] /. sol1}, {t, 0, 100}]

goes to nearly zero so quickly.

 

[mardusj]

That's correct what you said in the beginning about rearranging the equation. They're all independent.

Regarding the values of r, d, and m, I know the values of these per 1000 inhabitants.
Birth rate = 1.4/1000
Death rate = 4/1000
Net Migration Rate = 0.54/1000

Now, if I have the population in millions, it's easy to assume I should have these also in millions, r being 140, d 4000, and m 540? (there was a typo above, with r 1400 instead of 140). What I am confused about though is the time scale. Check the attachement - I know it's wrong, but it's getting the shape at least. How could we interpret the x-axis..?

If 82 is in millions, then r should be 140, d 400, m 540, and the time scale to see the graph would be 0-0.002... how should the x-axis be interpreted, because these are certainly not years.. :S

The trend should be going down, but certainly -2060 million a year wasn't correct...

Now, this is the first part. The second step should be an inspection of the age groups: 20-64 & 65+. The model could work for the first age group, but what is missing for the second group though (and I don't know how to incorporate it in the model) is the inflow of the aging people from the younger group. I don't know how to estimate it, and it is the most crucial number, which causes in the future the older group to grow significantly, as compared to the 20-64, which is supposed to shrink.

Thanks in advance for your help!

Thomas

 

[Bill Simpson]

Your latest thumbnail has x=82 so everything will be in terms of millions.
k=10000000 so your carrying capacity is ten million million.
r=.14 so 140000 births per year.
d=.4 so 400000 deaths per year.
m=.054 so 54000 immigration in per year.

If I assume k should be 100, but that is just guessing.

In[4]:= (r-d+m)/(1-82/k)/.{r->1400,d->4000,m->540,k->100}

Out[4]= -11444.4

Something is really wrong with that slope.

Shouldn't that slope for the first year be roughly (1400-4000+540)/(82 Million) =~ -1/40000 and not -11400 since you are not close to the carrying capacity.

And perhaps I'm just not reading carefully enough but your number for r seems to change again and again and again.

 

[mardusj]

It's way too steep that's for sure... ehm I'm losing faith -.-

at least the slope is negative... but no really, I have no clue now why. The parameters are fine, saturation seems okey. Do you have any idea?

 

[Bill Simpson]

When I can't make sense of a notebook I go back to the beginning and start step by step.

Your first post, if I approximate this with a single step of one year, gives

In[1]:= x[0]=100;r=1.4;k=100000;dx=r*x[0]*(1-x[0]/k)
Out[1]= 139.86

Your r says population will grow by 40% and that is about what it does, given a tiny offset of your carrying capacity.

But your k is 1000 times your current population and that worries me that the k value might be in error.
Or you might be thinking the carrying capacity could be 1000 times the current value. I cannot know.

Now see what NDSolve makes of this.

sol1 = NDSolve[{D[x[t], t] == r*x[t](1 - x[t]/k), x[0] == 100} /. {r -> 1.4, k -> 100000}, x[t], {t,0, 100}];
Plot[x[t] /. sol1, {t, 0, 100}, PlotRange -> All]

The result is a nice sigmoid that rapidly approaches your carrying capacity of 100000.

So this seems to say that your original equation perhaps has some hope and perhaps the difficulty lies only in the coefficients.

Now I go to the next post you made with a screenshot.
Note your population has changed and carrying capacity has changed and rates have changed 1000 fold.

sol1 = NDSolve[{D[x[t], t] == (r - d + m)*x[t](1 - x[t]/k), x[0] == 82} /. {r -> 1400, d -> 4000, m -> 540, k -> 100}, x[t], {t, 0, 100}];
Plot[x[t] /. sol1, {t, 0, 100}, PlotRange -> All]

The graph shows nothing so try a Table

In[16]:= Table[{t,x[t]/.sol1},{t,0,100}]
Out[16]= {{0, 82.}, {1, 1.8810672650496587`*^-16}, {2, 4.783111657858754`*^-20}, {3, 1.154702315260421`*^-20},etc}

So the decline in a fraction of a year goes to approximately zero, but your rates are 1000x what the were.

Put the rates back and shorten up the period to try to stretch the beginning of the curve

sol1 = NDSolve[{D[x[t], t] == (r - d + m)*x[t](1 - x[t]/k), x[0] == 82} /. {r -> 1.4, d -> 4, m -> .54, k -> 100}, x[t], {t, 0, 5}];
Plot[x[t] /. sol1, {t, 0, 5}, PlotRange -> All]

And there is a nice sigmoid going towards zero as expected.

Now your third post where the rates and k change again, but population doesn't change.

sol1 = NDSolve[{D[x[t], t] == (r - d + m)*x[t](1 - x[t]/k), x[0] == 82} /. {r -> .14, d -> .4, m -> .054, k -> 10000000}, x[t], {t, 0, 40}];
Plot[x[t] /. sol1, {t, 0, 40}, PlotRange -> All]

We get a nice sigmoid as expected.
It isn't possible to verify that carrying capacity is approached because we are going to zero. But k==10000000 seems out of line with x[0]==82.
And it is difficult for me to rationalize Birth rate=1.4/1000 with r->.14.

My guess at this point is that going through and carefully verifying that all the "units" are correct might make this work for you.
I do not have the source of your statistics at hand so I can't do that for you.

 

[mardusj]

Hi Bill,

once again thanks for your reply, apologies for me answering only now, I've been extremely busy.

So, apparently the statistics that I was given were not correct. It should be now as following:

Birth rate (per 1000): r=8.3
Death rate (per 1000): d=10.92
Net Migration rate (per 1000): m=0.54
Population (in Mi): x[0]=82
Carrying Capacity (in Mi): k=100-120 (rough estimation)

So, if I properly insert the values in Millions, the code should looks as following:
r->8300
d->11000
m->540
x[0]=82
k=100-120

The curve I am getting is nicely shaped I think. However, what concerns me is again the time axis. The rates above are per 1000/a year, so how would the scaling of the x-axis to such small number be interpreted? Any ideas, guesses on the new results?

 

[Bill Simpson]

Here are two examples using your latest statistics. In the second I use your prescaling of all your values and in the first I don't do that. Since your rates are small compared to the size of the country I use discrete steps of one year, to avoid any question about the time scale used in NDSolve, and we can then compare that to your NDSolve results.

In[1]:= r=8.3/1000;d=10.92/1000;m=.54/1000;k=100*10^6;x=82*10^6;
For[year=1,year<10,year++,
dx=(r-d+m)*x(1-x/k);
x=x-dx;Print[{x,dx}];
]

From In[1]:= {8.20307*^7, -30700.8}
From In[1]:= {8.20614*^7, -30659.9}
From In[1]:= {8.20920*^7, -30619.0}
From In[1]:= {8.21226*^7, -30578.2}
From In[1]:= {8.21531*^7, -30537.3}
From In[1]:= {8.21836*^7, -30496.5}
From In[1]:= {8.22140*^7, -30455.7}
From In[1]:= {8.22445*^7, -30414.9}
From In[1]:= {8.22748*^7, -30374.1}

In[3]:= r=8300;d=10920;m=540;k=100;x=82.;
For[year=1,year<10,year++,
dx=(r-d+m)*x(1-x/k);
x=x-dx;Print[{x,dx}];
]

From In[3]:= {30782.8,-30700.8}
From In[3]:= {-1.96456*^10, 1.96457*^10}
From In[3]:= {-8.02777*^21, 8.02777*^21}
From In[3]:= {-1.34046*^45, 1.34046*^45}
From In[3]:= {-3.73740*^91, 3.73740*^91}
From In[3]:= {-2.90538*^184, 2.90539*^184}
From In[3]:= {(-1.75577*^370, 1.75577*^370}
From In[3]:= {(-6.41208*^741, 6.41208*^741}
From In[3]:= {(-8.55187*^1484, 8.55187*^1484}

Now, unless I'm making some serious mistake, I think this is showing the unscaled statistics give sensible results, you are loosing a few thousand people each year, magnified a bit by your carrying capacity contribution.

This unscaled NDSolve seems to show the same result

r = 8.3/1000; d = 10.92/1000; m = .54/1000; k = 100*10^6; T = 200;
sol1 = NDSolve[{D[x[t], t] == (r - d + m)*
x[t](1 - x[t]/k), x[0] == 82*10^6}, x[t], {t, 0, T}];
Plot[x[t] /. sol1, {t, 0, T}, PlotRange -> All]

So it appears there is a very serious problem between your scaling and my unscaling.

Can you resolve this? If you look at In[3] I think you can see you are subtracting rates of thousands from a population of hundreds if I haven't made a mistake. Perhaps your rate is 8300/10^6.

 

[mardusj]

Thank you Bill.

I have now come to an end, I guess. Your last suggestion seems to have worked out best. I have plotted the final solutions in Matlab. You can see them attached for your own interest (?).

I will be presenting my results on Wednesday.

p.s. I also had to work out two age groups, 20-64, and 65+

My model for these was as following:

20-64: inflow from 0-19 cohort + total net migration - death rate - outflow to 65+ cohort

65+: total net migration - death rate + inflow from 20-64 cohort

For the rates I used some assumptions:

-for inflows and outflows from and to cohorts I looked at dependency rations, old and young, which in this case were 31 (per 1000), and 2 (per 1000);

-total net migration in Germany = 0.54; 0.50 out of it goes to 20-64, and 0.04 to 65+ (neglect the young group)

-death rate in Germany = 11; 3 goes to 20-64, and 8 goes to 65+ (again neglect the young group)

These are general assumptions out of the blue, but are sensible I think.Cheers man!