- #1
ENGRstudent
- 26
- 0
So, here's the deal:
The professor that normally handles Electronics 1 and Electronics 2 went on sabbatical for a year, so the engineering department brought in a guest lecturer to handle it during his absence. The original electronics professor would do op-amps in electronics 1, and BJT's and FETs in electronics 2. The guest lecturer came in and did only BJT's in electronics 1, and now that the resident instructor is back from sabbatical, he's doing BJT's and FETs.
We told him that we hadn't covered a single practical op-amp yet, so he's been trying to use or lab time to condense an entire semester of op-amps into 3 hour periods on wednesday afternoons.
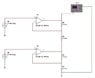
He gave us the attached homework problem on op-amps. What he told us was:
The CMRR of Op-Amps 1 & 2 are equal and are finite.
A) What is the expression for V_out
B) What is the relationship between the various resistors for the output to be proportional to the difference of V1 and V2?
V_out is taken at the node right above R1, as shown by the oscilloscope.
I'm not entirely certain how to approach this problem. In all the examples we've worked in class, I've never seen an op-amp circuit connected this way.
Any help you could give would be greatly appreciated.
No values were given; he wants the answer in algebraic form.
The professor that normally handles Electronics 1 and Electronics 2 went on sabbatical for a year, so the engineering department brought in a guest lecturer to handle it during his absence. The original electronics professor would do op-amps in electronics 1, and BJT's and FETs in electronics 2. The guest lecturer came in and did only BJT's in electronics 1, and now that the resident instructor is back from sabbatical, he's doing BJT's and FETs.
We told him that we hadn't covered a single practical op-amp yet, so he's been trying to use or lab time to condense an entire semester of op-amps into 3 hour periods on wednesday afternoons.
He gave us the attached homework problem on op-amps. What he told us was:
The CMRR of Op-Amps 1 & 2 are equal and are finite.
A) What is the expression for V_out
B) What is the relationship between the various resistors for the output to be proportional to the difference of V1 and V2?
V_out is taken at the node right above R1, as shown by the oscilloscope.
I'm not entirely certain how to approach this problem. In all the examples we've worked in class, I've never seen an op-amp circuit connected this way.
Any help you could give would be greatly appreciated.
No values were given; he wants the answer in algebraic form.