How Do You Calculate the Required Mass and Position to Balance a Rotating Shaft?

[LDC1972]

Homework Statement

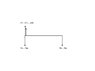
A shaft rotates at 1500rpm between 2 bearings, Ra and Rb. Ra force is 5 Kn and Rb is 3 Kn.
A single mass is to be used to balance the shaft, to give reactions of zero.
Mass to be placed at 90 degrees to shaft and at 200 mm radius.

What is the required mass and position?

Homework Equations

I have done the following:

For equilibrium, the bearing reactions = 8 Kn so balance weight must be 8 Kn too. BUT, as the weight is non central (200 mm radius (and we can then assume shaft diameter at 400 mm)),

So, Ra = mass x position length / shaft length = 8 x position length / 200 x 1000 = 5 KN

Ra = 1000 / 8000 = 0.125

Ra = 8 x 0.125 / 0.2 x 1000 = 5 Kn

Then taking moments about Rb gives 3 Kn which is correct.

The Attempt at a Solution

Knowing Ra = 5 Kn, Ra x 0.2m - 8 Kn x distance = 0 for equilibrium

So,

Ra x 0.2 m - 8 kn x unknown distance = 0
Ra = 8 x 125 / 200 x 1000 = 5 Kn

∴ mass should be 8 Kn 125 cm from Rb.

BUT, have I neglected the angular rotation wr? As the weight is 200 mm out from shaft centre?

And if so, then Mc Rc = mr

So I get Mc Rc = 8 Kn x 0.2 m = 1.6 Kg.

So final answer weight of 1.6 Kg should be placed at 200 mm radius (outer edge of shaft at 180 degrees to bearing reactions) at position 125 cm from Rb (bearing B of 3 Kn).

I apologise if this is messy but I'm struggling a bit here and pointers or a "yes well done" would be simply fantastic, I really appreciate the time you guys spend helping!

Thank you!

 

[CWatters]

BUT, have I neglected the angular rotation wr? As the weight is 200 mm out from shaft centre?

And if so, then Mc Rc = mr

So I get Mc Rc = 8 Kn x 0.2 m = 1.6 Kg.

Your working looks wrong but I got same answer (1.62kg) using the equation for centripetal force..

F=mrω²=8kN

ω=1500rpm=157.1 rads/s
r=0.2m

solve for m.

 

[CWatters]

at position 125 cm from Rb (bearing B of 3 Kn).

I get a different answer for the position along the bar. It's clear the mass has to be nearer the end with the highest out of balance force (the Ra 5kn end) order to provide more counter balance force that end. Try summing the moments about the middle of the bar...

 

[LDC1972]

Thanks for the very fast reply, I'm still hammering away. I really thought I'd cracked this :-(

 

[LDC1972]

I get a different answer for the position along the bar. It's clear the mass has to be nearer the end with the highest out of balance force (the Ra 5kn end) order to provide more counter balance force that end. Try summing the moments about the middle of the bar...

I'm so confused :-(

I'm doing the equation as follows:

Ra = 5 Kn (we know this).

So:

Ra = 1.62 kg x 617 cm / 200cm x 1000 = 5 Kn.

BUT the shaft is only 200cm long, so my 617cm is madness...

Please help. I'm following an example in the book exactly as above, but there's works!

 

[LDC1972]

Is it not possible the position is as per 8 Kg but the actual weight due to radius is only 1.62 Kg?

 

[CWatters]

There are two parts to the problem..

1) Calculating the mass needed.
2) Working out it's position along the rod.

For part 1: The centripetal force of the new mass must be equal and opposite to the centripetal force caused by the out of balance shaft. You correctly calculated that this is 8000N. You know the speed and radius of the counterbalance so you can calculate the mass = 1.62kg.

For Part 2: You need to calculate where along the shaft the counter balance goes. See my diagram above..

Assume:

Rod is length 2m
Clockwise is +ve
X = distance from centre

Summing the moments around the middle of the rod gives...

-5*1 + 8*X + 3*1 = 0

-5 + 8*X + 3 = 0

8*X = 2

X = 0.25m

 

[CWatters]

If you want you can sum the moments about the Ra end...

Assume Y = distance from Ra end..

3*2 - 8*Y = 0

6 - 8Y = 0

Y = 6/8 = 0.75m

or 0.25 from the middle. This is the same position as I calculated above.

 

[LDC1972]

There are two parts to the problem..


Summing the moments around the middle of the rod gives...

-5*1 + 8*X + 3*1 = 0

-5 + 8*X + 3 = 0

8*X = 2

X = 0.25m

It was "summing the moments that threw me. I've done it right t the start of the course for beams, but something didn't "click". I've managed to get a migraine now (been at ti since 4:30am and it's now 11am!)

So I'll be back in an hour and follow your moments properly.

The course I'm doing is level 5, and so far I've flown through it, but we have to do one level 6 and this is causing me troubles... Still only one more question left after this one and back to level 5 :-)

Thanks so much for your help!

 

[LDC1972]

If you want you can sum the moments about the Ra end...

Assume Y = distance from Ra end..

3*2 - 8*Y = 0

6 - 8Y = 0

Y = 6/8 = 0.75m

or 0.25 from the middle. This is the same position as I calculated above.

There's a second and final part to this problem and just wanted to run past you guys my solution to see if I've done OK?

Exact same system except now to be balanced by 2 masses, 0.5m from each end and radius now 100mm.

I have done:

Shaft length = 2 m
157.1 rad/s
Ra = 5 Kn
Rb = 3 Kn
r = 100mm

Used F = mrw^2 twice, one for M1 and one for M2:

M1:
F = M1rw^2 = 5 Kn
F = m * 2468.041 = 5 Kn
∴ M1 = 2.023 Kg

Did same for M2 and got 1.216 Kg

Hopefully that's good and I can put this to rest?!

Many thanks as always...

 

[LDC1972]

I think I've changed me mind...

Going back to Ra = mass x position length / shaft length = 8 x position length / 200 x 1000 = 5 KN

Ra = 1000 / 8000 = 0.125

Ra = 8 x 0.125 / 0.2 x 1000 = 5 Kn

And using new figures gives:

Ra = mass x position length / shaft length = 20 kg x 0.5 m / 2 m = 5 KN

So mass 1 = 20 kg

Rb = mass x position length / shaft length = 4 kg x 0.5 m / 1.5 m = 3 KN

So mass 2 = 4 kg

Although these masses seem too big to be true...

I wish our instructional book even scratched the surface of this problem!

 

[CWatters]

I have a feeling it might not be possible to exactly balance out the shaft as there are two possibly conflicting requirements...

1) The forces must balance in all planes. eg the total radial force must still sum to zero.. The two balance weights together must still produce a total force of 8kN.

If m = m1+m2 then..

0.5*m*r*ω² = 8000

Gives m = m1 + m2 = 6.48kg (Edit: However I think one force/mass might have to be -ve, see below)

2) Then looking look at the moments...

Let F1 be the force produced by m1 etc

About Ra..

-0.5*F1 - 1.5*F2 + 2*Rb = 0

About Rb..

1.5*F1 + 0.5*F2 - 2*Ra = 0

Two equations, two unknowns so can be solved for the forces F1 and F2 and then the two masses can be calculated.

However when I tried to do that just now I got a -ve force for at least one of them. I think that will mean one mass has to be set 180 degrees around from the other?

It's nearly midnight here so I may have made a mistake. I'm off to bed. If I get chance I'll have another go tomorrow.

 

[LDC1972]

I have a feeling it might not be possible to exactly balance out the shaft as there are two possibly conflicting requirements...

1) The forces must balance in all planes. eg the total radial force must still sum to zero.. The two balance weights together must still produce a total force of 8kN.

If m = m1+m2 then..

0.5*m*r*ω² = 8000

Gives m = m1 + m2 = 6.48kg (Edit: However I think one force/mass might have to be -ve, see below)

2) Then looking look at the moments...

Let F1 be the force produced by m1 etc

About Ra..

-0.5*F1 - 1.5*F2 + 2*Rb = 0

About Rb..

1.5*F1 + 0.5*F2 - 2*Ra = 0

Two equations, two unknowns so can be solved for the forces F1 and F2 and then the two masses can be calculated.

However when I tried to do that just now I got a -ve force for at least one of them. I think that will mean one mass has to be set 180 degrees around from the other?

It's nearly midnight here so I may have made a mistake. I'm off to bed. If I get chance I'll have another go tomorrow.

The masses are definitely on the same plane (not 180 degree opposed)

Thank so much for trying this one so hard for me! I like me original answer, because the values look reasonable, but my second answer the values look ridiculous!

Wish I could contribute intelligently, but I'm beyond the envelope here!

 

[CWatters]

I like me original answer, because the values look reasonable..

They do but I think the approach is wrong.

M1:
F = M1rw^2 = 5 Kn
F = m * 2468.041 = 5 Kn
∴ M1 = 2.023 Kg

You appear to be assuming that F1 and F2 must equal Ra and Rb.

I believe F1 and F2 must sum to 8kN but they won't be the same value as Ra and Rb because they don't act in the same place as Ra and Rb. In addition (I know some problems contain information that isn't needed but) you haven't used the information that the masses are "0.5m from each end".

If you assume F1 = 5kN, and F2=3kN and look at the moments you will find they don't sum to zero - which means there will still be a load at the bearings.

I have worked out a solution which appears satisfy both conditions. Will post that in a few moments when I have done the diagram.

 

[CWatters]

Ok there are two conditions which I think have to be met..

1) F1 + F2 must sum to 8000N
2) The moments must sum to zero.

So first equation is... F1 + F2 = 8000 .....(1)

For the second condition take the moments about the middle and you get...

1*Rb + 0.5*F1 - 0.5*F2 - 1*Ra = 0

Rearrange that and you get

F1 - F2 = 2(Ra -Rb) = 6000 .... (2)

Now you have two equations and two unknowns.

Solving them gives

F1 = 6857N
F2 = 1143N

As a double check.. These add up to 8000N

Then using F = mrω² on each gives

M1 = 2.78Kg
M2 = 0.46Kg

 

[LDC1972]

Ok there are two conditions which I think have to be met..

1) F1 + F2 must sum to 8000N
2) The moments must sum to zero.

So first equation is... F1 + F2 = 8000 .....(1)

For the second condition take the moments about the middle and you get...

1*Rb + 0.5*F1 - 0.5*F2 - 1*Ra = 0

Rearrange that and you get

F1 - F2 = 2(Ra -Rb) = 6000 .... (2)

Now you have two equations and two unknowns.

Solving them gives

F1 = 6857N
F2 = 1143N

As a double check.. These add up to 8000N

Then using F = mrω² on each gives

M1 = 2.78Kg
M2 = 0.46Kg

Wow, I've been trying for hours again and your help is amazing. Thank you so much!

 

[CWatters]

No problem, it was interesting.

It's easy to prove that the masses must be positioned and split so the moments also to sum to zero...

Consider what happens if you put both masses very close to one end (for example at Ra)? The force they produce still sums to 8kN but the load on the Ra bearing will be 8000-5000 = 3000N.

 

[LDC1972]

I am in awe! And you've taught me a lot which is what it's all about really eh :-)

 

[Big Jock]

I am working through this question also and was looking to confirm that in post #7 that the answer is the mass is 1.62kg and a=0.25m b=0.75m. Is that correct? If so why doesn't a and b add up to the length of the shaft at 2m?
Very confused!

 

[LDC1972]

I am working through this question also and was looking to confirm that in post #7 that the answer is the mass is 1.62kg and a=0.25m b=0.75m. Is that correct? If so why doesn't a and b add up to the length of the shaft at 2m?
Very confused!

Sorry Jock, this post isn't going to help you much! I got this question wrong entirely.

I never looked at it again after so can't help at all!

After that module it was indeed back to zooming through modules though as they are a lower level! I highly advise choosing the hydraulic module for a lovely math break next if you need one ;-) (assuming you're doing mechanical)

I'm on module 5 now and managed distinctions for first 4 :-D

Good luck pal.

Cheers and good luck!

 

[Big Jock]

The mass is correct though I know that much but I can't for the life of me get the positions worked out.
This set of questions are especially hard!
Take it you still have to complete this then?

 

[LDC1972]

The mass is correct though I know that much but I can't for the life of me get the positions worked out.
This set of questions are especially hard!
Take it you still have to complete this then?

No I got a merit for that exam, just got Q2 wrong.
Unfortunately the feedback just said "incorrect" so can't help!
For the whole module I got a distinction as the other 3 TMA's were graded at distinction.

 

[Big Jock]

I would gladly take a pass for this now just get it complete and move onto something else. I sent you a private message if you can help I will send a private message with my email

 

[LDC1972]

I would gladly take a pass for this now just get it complete and move onto something else. I sent you a private message if you can help I will send a private message with my email

I know that feeling! At least after this unit it becomes way more sensible.
PM'd...

 

[Keston Harrison]

Ok there are two conditions which I think have to be met..

1) F1 + F2 must sum to 8000N
2) The moments must sum to zero.

So first equation is... F1 + F2 = 8000 .....(1)

For the second condition take the moments about the middle and you get...

1*Rb + 0.5*F1 - 0.5*F2 - 1*Ra = 0

Rearrange that and you get

F1 - F2 = 2(Ra -Rb) = 6000 .... (2)

Now you have two equations and two unknowns.

Solving them gives

F1 = 6857N
F2 = 1143N

As a double check.. These add up to 8000N

Then using F = mrω² on each gives

M1 = 2.78Kg
M2 = 0.46Kg

I was following this ok as a way of double checking my work, but surely for your equation 2, 2(Ra-Rb) = 2(5000 - 3000) = 4000 and not 6000 as quoted?

 

[CWatters]

Good catch. Looks like I made an error. Should be...

F1 - F2 = 2(5000 - 3000) = 4000.

That gives new values of F1 = 6000N and F2 = 2000N and the masses will be different.

 

[Keston Harrison]

Good catch. Looks like I made an error. Should be...

F1 - F2 = 2(5000 - 3000) = 4000.

That gives new values of F1 = 6000N and F2 = 2000N and the masses will be different.

Thanks. Thought I was losing it there.