- #1
xDk
- 8
- 0
Hello, I am having a bit of trouble understanding this diagram.
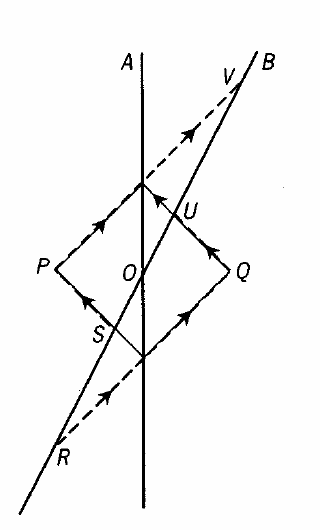
I can accept the example of the moving train with an observer beside the train and an observer on the train, then two lights emit from both ends of the train when the train pass the observer. But this diagram is a little confusing to me.
The description of the diagram reads: B sends out light rays RQU and SPV to illuminate the events P and Q. RU=SV and so these events are equidistant according to B. The signal RQ was sent out before the signal SP so B concludes event Q took place well before P.
The order of events for B is Q, then O, and then P.
My first issue is why is RQ sent out before SP.
Second issue is why are the events in the order Q then O then P for B.
I can accept the example of the moving train with an observer beside the train and an observer on the train, then two lights emit from both ends of the train when the train pass the observer. But this diagram is a little confusing to me.
The description of the diagram reads: B sends out light rays RQU and SPV to illuminate the events P and Q. RU=SV and so these events are equidistant according to B. The signal RQ was sent out before the signal SP so B concludes event Q took place well before P.
The order of events for B is Q, then O, and then P.
My first issue is why is RQ sent out before SP.
Second issue is why are the events in the order Q then O then P for B.