Hemisphere sliding down problem

[kevin0960]

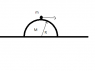
There is a small object, which mass is m on the top of hemisphere, with the mass of M.

the size of the object is neglectable. Also, the radius of hemisphere is R.

There is no friction between the hemisphere and the object, and the hemisphere and the surface. What if we slightly hit the object the object will be fall from the hemisphere.

At what point the mass will completely off from the hemisphere?

I attatched the the picture.
---

I first tried to use energy conservation law to find the velocity of the object.
$$\frac{1}{2} mv^2 + mgR(cos \theta) + \frac{1}{2}MV^2 = mgR$$

Also by conservation of momentum on x axis, we can deduct

$$mv_x = MV$$

But I just stucked at here. Plz someone help me

 

[kuruman]

Let's say that θ in the first equation represents the angle at which the mass flies off. That's one unknown. You also have the final velocities, V and v_x that are unknown. So you have three unknowns and only two equations. You need one more equation. What is the condition that must be satisfied if the mass is to fly off? That's your third equation.

 

[kevin0960]

I found few more equations for that problem.

First, because the object moves on the hemisphere before it falls off It must satisfy following condition

$$\frac{v_y}{v_x + V} = tan \theta$$

Also, I am not quite sure about the equation but since the object is having on circular motion (at the frame of hemisphere),
$$\frac{m((v_x + V)^2 + v_y^2)}{R} = mgcos\theta - N$$

and at the time the object falls from the hemisphere, N will be 0

Is this right??

 

[kuruman]

In these two equations, you need the horizontal velocity component relative to the hemisphere. I would write that as v_x - V to keep V an algebraic quantity. Then when you substitute for V using the momentum conservation equation, you would get v_x+(m/M)v_x in the expression. This voids confusion.

So you have four equations (sorry I said three earlier) and four unknowns. You can find an expression for θ in terms of the given quantities.

 

[paranormal]

Hello,

Thank you for providing the information and the attached picture. I can provide some insight on this problem.

Firstly, the problem can be approached using energy conservation and conservation of momentum, as you have already started to do. However, there are a few things to consider before solving the problem.

1. In the given problem, the object is initially at rest on top of the hemisphere. This means that the initial velocity of the object is zero. Therefore, the initial kinetic energy of the object is also zero.

2. The potential energy of the object at the top of the hemisphere is given by mgh, where h is the height of the object from the ground. However, in this problem, the height of the object is negligible compared to the radius of the hemisphere. This means that the potential energy of the object is also negligible.

3. Since there is no friction between the hemisphere and the object, the only external force acting on the object is gravity. Therefore, the work done by this force is equal to the change in kinetic energy of the object.

Considering these points, we can rewrite the energy conservation equation as:

mgR = \frac{1}{2}MV^2

This equation tells us that the velocity of the object at any point on the hemisphere is directly proportional to the square root of the mass of the hemisphere. Therefore, as the object slides down the hemisphere, its velocity will also increase.

Now, let us consider the conservation of momentum on the x-axis:

mv_x = MV

Since the object is initially at rest, its initial momentum is zero. Therefore, the momentum of the hemisphere must also be zero. As the object slides down the hemisphere, its velocity increases, but the velocity of the hemisphere remains constant. This means that the mass of the hemisphere must also increase to maintain the conservation of momentum equation.

Now, coming back to the question, at what point will the object completely fall off the hemisphere? This will happen when the velocity of the object becomes equal to the velocity of the hemisphere. At this point, the conservation of momentum equation will become:

mv_x = MV

where v_x is the velocity of the object and v is the velocity of the hemisphere. Solving this equation will give you the position at which the object will completely fall off the hemisphere.

I hope this helps. Good luck with your problem-solving!