- #1
sallama
- 5
- 0
I want to figure out critical speed of hollow shaft. When I calculate from equation, critical speed of this shaft is approximately 10000 RPM. But when I start to increase speed of shaft, at ~2500 RPM I see that the critical speed occured. What can I do to increase this critical speed to double, (to add mass under hollow shaft?). And what is the problem that I can not calculate real critical values. Assy Configuration, Fixed Shaft, Grooves, Length??
System can be seen at attachment. On the center axis of the shaft, a non turn shaft placed. On this shaft there are two 6308 Ball bearings to allow turn the hollow shaft. On the hollow shaft there are grooves.
Hollow Shaft info:
Material: Steel (I don't know exactly which type, but producer said that ST37/ASTM A283)
Do= 160mm
Di=129mm
Length (Center From Bearing)=1350mm
Total Length=1500mm
Distribution Force (approximate) =1500N
Fixed Shaft D=45mm
Bearing Type: Ball Bearing 6308Motor: 15 KW
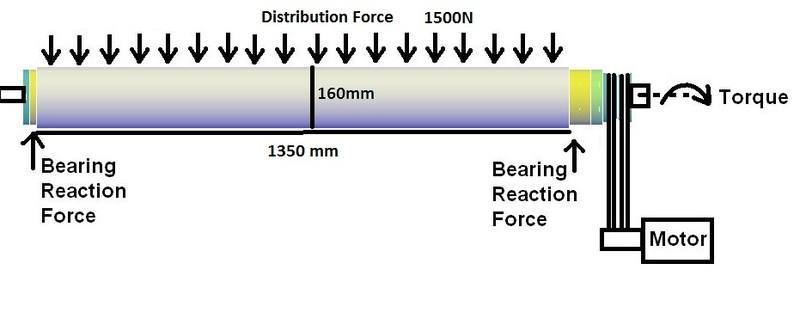
System can be seen at attachment. On the center axis of the shaft, a non turn shaft placed. On this shaft there are two 6308 Ball bearings to allow turn the hollow shaft. On the hollow shaft there are grooves.
Hollow Shaft info:
Material: Steel (I don't know exactly which type, but producer said that ST37/ASTM A283)
Do= 160mm
Di=129mm
Length (Center From Bearing)=1350mm
Total Length=1500mm
Distribution Force (approximate) =1500N
Fixed Shaft D=45mm
Bearing Type: Ball Bearing 6308Motor: 15 KW



