- #1
mathsciguy
- 134
- 1
I want to make a parallel plate capacitor without dielectric between it, that is, a capacitor with free space.
Can I do a working capacitor with just a two parallel cardboard coated in aluminum? I figured it should look like this:
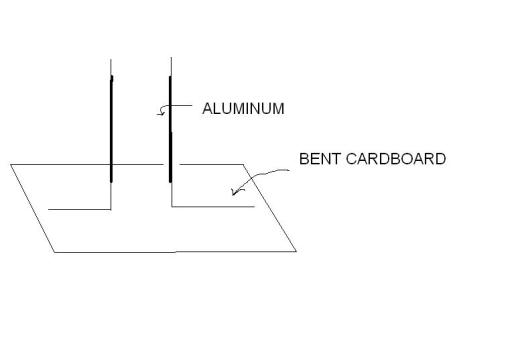
Also, if there's anyone who's got a better idea on how I could make this, I'd really appreciate it if you could share that.
Can I do a working capacitor with just a two parallel cardboard coated in aluminum? I figured it should look like this:
Also, if there's anyone who's got a better idea on how I could make this, I'd really appreciate it if you could share that.
Last edited: