- #1
ermines
- 45
- 0
well i hope someone knows how to solve this problem... 
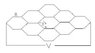
well you see in the picture that there is a honeycomd-like circuit...every line that comprises the honeycomb has a resistor with a resistance of R...meaning in a hexagon, there are six resistors...
the question is to find the total resistance or Req...and also the current (I) passing through the one i indicated in the drawing
sorry for the drawing if it is not to accurate...
i got the answer of 3R for the Req and one-third for the I...is this correct...actually what I'm looking for is the shortest solution that would solve the problem...maybe a two liner will be ...
thanks...
hmmmmmmm, i hope the pic would be posted soon...
well you see in the picture that there is a honeycomd-like circuit...every line that comprises the honeycomb has a resistor with a resistance of R...meaning in a hexagon, there are six resistors...
the question is to find the total resistance or Req...and also the current (I) passing through the one i indicated in the drawing
sorry for the drawing if it is not to accurate...
i got the answer of 3R for the Req and one-third for the I...is this correct...actually what I'm looking for is the shortest solution that would solve the problem...maybe a two liner will be ...
thanks...
hmmmmmmm, i hope the pic would be posted soon...
Attachments
Last edited: