How charges can flow in circuit wires at the same potential

[themagiciant95]

I have this simple circuit

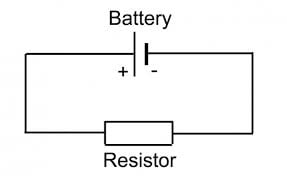I know that if a consider the wire from the + of the battery until the + extreme of the resistor, in this portion the wire has the same potential. The same thing regarding the portion of the wire beetween the - of the battery until the - of the resistor.
If this portions of wire are equipotential how can the charges flow in them? It seems like that the flow of charge (current) only happens in the resistor, where there is a Voltage drop

 

[cnh1995]

In circuit theory, we ignore the voltage across a wire since its resistance is 'assumed' to be zero. Practically, it is very small compared to the load resistance and a very small voltage is present across any section of wire.

 

[themagiciant95]

Nice. But, if the potential difference in the wire in very small compared to the one of the resistor, then the current cannot be the same in every part of the circuit.
Where am i wrong ?

 

[cnh1995]

Nice. But, if the potential difference in the wire in very small compared to the one of the resistor, then the current cannot be the same in every part of the circuit.
Where am i wrong ?

Do you know Ohm's law?

 

[sophiecentaur]

Do you know Ohm's law?

Ohm's Law only refers to Metals and at constant temperature. I think you are really referring to the definition of Potential Difference, which is the Work Done per unit charge.

 

[robphy]

Possibly useful:
https://matterandinteractions.org/wp-content/uploads/2016/07/SurfaceChargePoster.pdf
https://matterandinteractions.org/wp-content/uploads/2016/07/circuit.pdf
http://www.glowscript.org/#/user/ma...atterandinteractions/program/18-SurfaceCharge

 

[Mister T]

Nice. But, if the potential difference in the wire in very small compared to the one of the resistor, then the current cannot be the same in every part of the circuit.

Choose two points on the wire and the potential difference between those points is very small. The current $I$ that flows through that piece of wire equals $\frac{V}{R}$ where $V$ is that potential difference and $R$ is the resistance of that piece of wire.

Now choose two points, one on each side of the resistor and the potential difference between those points is much larger. The current $I$ that flows through that resistor equals $\frac{V}{R}$ where $V$ is that potential difference and $R$ is the resistance of that resistor.

The resistance of the resistor is much larger than the resistance of that piece of wire, the potential difference across the resistor is much larger than the potential difference across the resistor, but the current through them is the same.

Where am i wrong ?

It's better to not speak of the potential "in" a wire. You can have a potential at a point in the wire, and thus a potential difference between two points along a wire. It is okay, though, to speak of current in a wire. The reason is because the current is the same at every point along a wire, but the potential is not (assuming a current flows through the wire).

By the way, Ohm's Law is not the assertion that the current equals $\frac{V}{R}$. Rather, it's the assertion that as you change the potential difference $V$ between two points the current changes in proportion, in other words, the value of $R$ remains the same. Such a thing never actually happens, but in many cases it's a good approximation. In others, though, such as an incandescent light bulb, it's not.

 

[themagiciant95]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

 

[anorlunda]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

In circuit analysis, we don't allow charges to pile up. No excess plus, no excess minus at any node. If the current was different in different places in the circuit you showed, a pile up would result.

All of this is summed up in a recent PF Insights Article: The What and Why of Circuit Analysis Assumptions

 

[sophiecentaur]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

This is actually very easy to justify. If the current in were more than the current out there would be a build up of charge. Just work out the forces (Coulomb Force - look it up) if there happened to be just 1C difference along a wire 1m long. Check the exponent of ten! It is PRACTICALLY impossible. The easiest path for the charge is the other way round the circuit!

 

[Mister T]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

Conservation of charge.

 

[Dale]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

In addition to the other responses, Kirchoff’s current law also ensures that.

 

[Delta2]

The potential difference is needed in order to maintain stable current $I=V/R$ across a resistance R. If R is zero and potential difference is zero then ohm's law become $I=\frac{0}{0}$ . 0/0 form doesn't mean that the current is zero or the current is infinite, we simply can't determine. It might be zero or infinite or a constant finite value. What it is, it will be determined from other parts of the circuit (in your case from the part of the circuit that contains the resistor).

Another more simple intuitive explanation is that the PD(Potential Difference) is needed in order to "overcome" the difficulties in flow of charges imposed by a resistance. If the resistance is zero then there are no difficulties imposed in the flow of charges, the charges can move freely without the need for the presence of a PD.

 

[themagiciant95]

I try to synthesize my interpretation from your fantastic insights.

In the simple circuit i showed in my question, we know the intensity of the current by the resistor and in particularly using the "ohm's law".
The 2 wires that connect the battery to the resistor has an uniform voltage, respectively of +V and -V, for this reason ( and for the fact that the wire can be seen having a cylindrical simmetry) the 2 wires have the same charge density. As the 2 wires have a uniform potential(+V and -V), we can derive the "charge conservation" law and say that the current is constant throght the circuit.

But, if the V were not uniform throght the wires, the charge distribution in them will be not uniform. What assures that the wires mantain an uniform voltage ?

 

[Dale]

But, if the V were not constant throght the wires, the charge distribution in them will be different. What assures that the wires mantain an uniform voltage ?

I don’t understand your question. If you are considering the assumption that V is not constant then you are (by assumption) assured that the voltage is not uniform.

 

[themagiciant95]

I don’t understand your question. If you are considering V is not constant then you are by assumption assured that the voltage is not uniform.

I corrected my question

 

[Dale]

I corrected my question

Hmm, the correction didn’t address my confusion. Your question is self contradictory. You start out with the assumption “if the V were not constant” but then ask about how “the wires mantain an uniform voltage”. If you assume that V is not constant then the wires can not maintain a uniform voltage as that would contradict the assumption

 

[anorlunda]

The reason why I wrote the PF Insights article The What and Why of Circuit Analysis Assumptions was to discourage people from trying to mix circuit analysis with deeper physical reasoning; especially conduction in a wire, flow of electrons and fields.

To understand what is happening with conduction, you need the free electron model which includes quantum effects. To understand fields and charges, you need Maxwell's Equations, and the size, shape and orientation of circuit elements is critical.

In circuit analysis, like the OP's example, we deliberately make simplifying assumptions that ignore charges, fields, and especially electrons. That allows us to use useful tools like Ohm's Law, and Kirchoff's Laws.

If you try to mix these things, conduction/fields/charges/closed-circuits you create a quagmire of confusion that is hard to overcome. My advice is to not try. Study circuit analysis, Maxwell's equations, Quantum Mechanics as separate subjects if you are motivated.

 

[themagiciant95]

The assumption is that the wires has an uniform voltage. My question is what principle assure that we can approximate that the wires have an uniform voltage ?

 

[anorlunda]

The assumption is that the wires has an uniform voltage. My question is what principle assure that we can approximate that the wires have an uniform voltage ?

In circuit analysis we define a wire as having zero resistance and uniform voltage. All the other components are similarly idealized devices that deliberately ignore some of the physics complications. Please read the article.

 

[cnh1995]

The assumption is that the wires has an uniform voltage. My question is what principle assure that we can approximate that the wires have an uniform voltage ?

If what you mean by voltage is 'potential difference', the wires are assumed to have zero voltage across them. You need to clear up the terminology first. Refer another one of anorlunda's great insights for this issue.
https://www.physicsforums.com/threads/tiny-tweak-in-teaching-basic-circuits.908496/

If you mean 'potential' by the term voltage, I believe tbe answer is already given by delta² in #13. Wires are assumed to have zero resistance, so no electric field is required to maintain the current. No field, no potential 'difference', hence, 'constant' potential throughout the wire.
Edit: Sorry, the thread I linked was a 'featured thread' and not an insights article.

 

[Dale]

The assumption is that the wires has an uniform voltage. My question is what principle assure that we can approximate that the wires have an uniform voltage ?

If you assume that the wire has a uniform voltage (which is the usual assumption) then you are automatically assured that the wire has a uniform voltage by that assumption!

What you may be asking is under what conditions that assumption is approximately valid when modeling a real circuit. That condition is when the resistance of the wire is very low. If the resistance is so low that the voltage drop is negligible then you are justified in making the assumption when modeling that circuit

 

[anorlunda]

Perhaps this will help. The picture below shows the equivalent circuit we use in circuit analysis to represent a real physical piece of wire. The OP is wondering about the resistance of a real wire R. If he continues his studies, he'll eventually discover that the L, C, and G terms are also nonzero in real life.

So, we can use this equivalent circuit to represent every segment of real life wire. But then we use Circuit Analysis (CA) to solve the whole thing. And the CA presumes that all the components are idealized and divorced from the physics. CA is a very powerful calculation technique. It is not physics.

Please read the article before posting more questions.

 

[themagiciant95]

Thanks so much

 

[sophiecentaur]

If you try to mix these things, conduction/fields/charges/closed-circuits you create a quagmire of confusion that is hard to overcome

This says it all. People need to learn to walk before they try to run. Extrapolating from little knowledge cannot take a student very far.

 

[Mister T]

The assumption is that the wires has an uniform voltage. My question is what principle assure that we can approximate that the wires have an uniform voltage ?

The resistance of the wires is negligible in comparison to the resistors and other circuit elements.

 

[Altair Tans]

That's very nice. The puzzle is almost complete. But what assures that the current is constant throght all the circuit

Say in a segment (current flowing from left to right) at a time to its left current is high and to its right its less...
So to conserve charge, some charge stays at the junction....
Now due to this piled up charge electric field will now push the charges on its left opposing their flow and push those on its right to support their flow...
The higher current eventually falls down and the lower current Eventually rises up...

This happens till they are again equal

 

[sophiecentaur]

This happens till they are again equal

When there's any change, an EM wave flows. That's the way to look at it.