- #1
westerman16
- 8
- 0
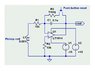
For a planning exercise i have to calibrate a hall probe to measure the magnetic flux density mid-way between opposite poles of two permanent bar magnets.
anyone know how to calibrate a hall probe so that i can do this experiment?
anyone know how to calibrate a hall probe so that i can do this experiment?