How to choose a random walk to best model diffusion?

[Jarek 31]

TL;DR Summary

local vs global entropy maximization?

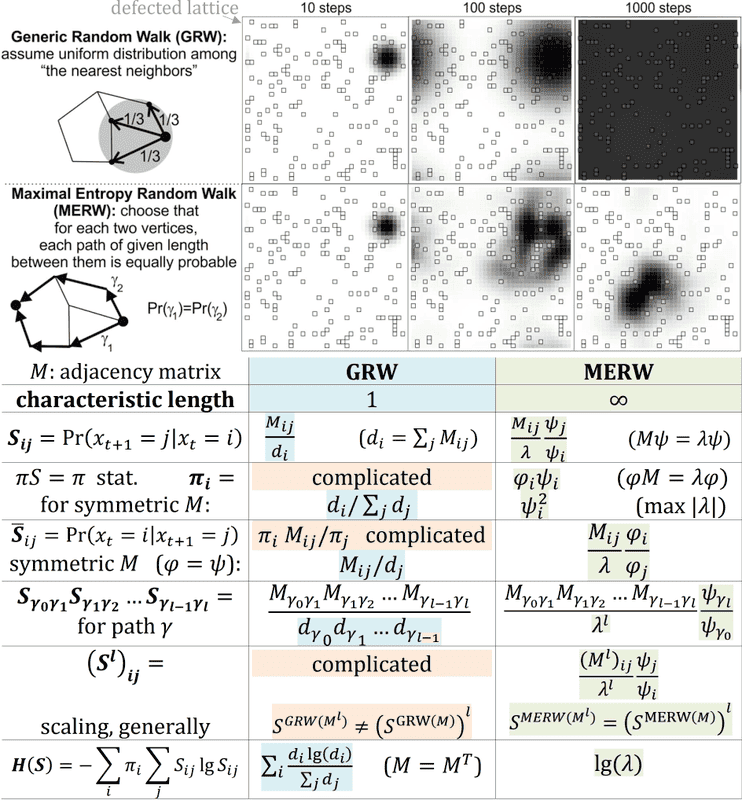
To choose random walk on a graph, it seems natural to to assume that the walker jumps using each possible edge with the same probability (1/degree) - such GRW (generic random walk) maximizes entropy locally (for each step).
Discretizing continuous space and taking infinitesimal limit we get various used diffusion models this way.

However, looking at mean entropy production: averaged over stationary probability distribution of nodes, its maximization leads to usually a bit different MERW: https://en.wikipedia.org/wiki/Maximal_entropy_random_walk

It brings a crucial question which philosophy should we choose for various applications - I would like to discuss.

GRW
- uses "local" approximation of (Jaynes) https://en.wikipedia.org/wiki/Principle_of_maximum_entropy
- has no localization property (nearly uniform stationary probability distribution),
- has characteristic length of one step - this way e.g. depends on chosen discretization of a continuous system.

MERW
- is the one maximizing mean entropy, "most random among random walks",
- has strong localization property ( https://en.wikipedia.org/wiki/Anderson_localization ) - stationary probability distribution exactly as quantum ground state,
- is limit of characteristic step to infinity - is discretization independent.

Simulator of both for electron conductance: https://demonstrations.wolfram.com/ElectronConductanceModelsUsingMaximalEntropyRandomWalks/
Diagram with example of evolution and stationary denstity, also some formulas (MERW uses dominant eigenvalue):

 

[eljose79]

https://en.wikipedia.org/wiki/Maximal_entropy_random_walkThank you for bringing up this interesting topic for discussion. it is important to carefully consider the philosophical implications of the models we use in our research. In the case of random walks on graphs, the choice between GRW and MERW can have significant implications for the results and interpretations of our studies.

First, I agree with your statement that GRW, with its assumption of equal probability for each edge, can be seen as a local approximation of the principle of maximum entropy. This approach may be suitable for certain applications, especially if the graph is highly connected and the edges have similar properties. However, as you mentioned, GRW does not have a localization property and can lead to a nearly uniform stationary probability distribution. This can be problematic if the underlying system has non-uniform distributions or if we are interested in studying the behavior of specific nodes in the graph.

On the other hand, MERW, with its goal of maximizing mean entropy, can be seen as the "most random" among random walks. This approach may be more suitable for applications where we want to capture the overall randomness of the system. Furthermore, the strong localization property of MERW, which leads to a stationary probability distribution similar to the quantum ground state, can be advantageous in studying systems with localized behavior.

It is also interesting to note the difference in the characteristic length of a step between GRW and MERW. While GRW has a characteristic length of one step, MERW approaches infinity as the limit of the characteristic step. This can have implications for the accuracy of the model, as it may depend on the chosen discretization of a continuous system.

In terms of practical applications, I think it would be valuable to carefully consider the choice between GRW and MERW based on the specific research question and the characteristics of the underlying system. For example, in the field of electron conductance, as demonstrated in the simulator you shared, MERW may be a more suitable model due to its localization property and its ability to capture the overall randomness of the system.

Thank you for sharing these insights and resources, and I look forward to further discussion on this topic.