How to deal with colour indices on spinors

[weningth]

I want to calculate transition amplitudes in QCD for processes like $q(k)q^\prime(p)\rightarrow q(k^\prime)q^\prime(p^\prime)$, where $q,q^\prime$ are quarks. However, I am unsure what to do with the colour indices of the quark spinors upon squaring the matrix element. For the sake of illustration let us consider the scattering mentioned above. The Feynman diagram including the colour indices $i,j,k,l$ and the adjoint indices of the gluon $a,b$ is shown below. The spin indices are suppressed.

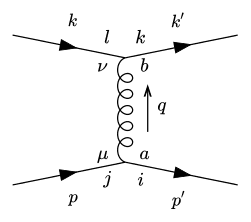
When I calculate the matrix element $i\mathcal{M}$, I get the following result:
$$i\mathcal{M}=\left[\bar{q}^\prime_i(k^\prime)igt^a_{ij}\gamma_\mu q^\prime_j(k)\right]
\frac{-ig^{\mu\nu}\delta_{ab}}{t}
\left[\bar{q}_k(p^\prime)igt^b_{kl}\gamma_\nu q_l(p)\right]
=ig^2t^a_{ij}t^a_{kl}\frac{1}{t}\left[\bar{q}^\prime_i(k^\prime)\gamma_\mu q^\prime_j(k)\right]\left[\bar{q}_k(p^\prime)\gamma^\mu q_l(p)\right],$$
where $t=q^2=(p-p^\prime)^2$.

Now, upon squaring the matrix element, I am not sure what happens with the colour indices $i,j,k,l$. Since they are summed over, one should assume that I would have to introduce another set of colour indices $m,n,o,p$ and one new adjoint index $b$ since $a$ is also summed over, as one does for the spacetime indices $\mu,\nu$ on the Dirac matrices. However, the standard result in most of the textbooks is that somehow we end up with the traces $tr[t^at^{a\ast}]=C_F(N^2-1)$ and the same for $b$, while the spinors $q,q^\prime$ somehow lose their colour indices, i.e. the squared matrix element (not averaged over spin and colour) looks like
$$|\mathcal{M}|^2=\frac{g^4}{t^2}\times C^2_F(N^2-1)^2
\times tr\left[\gamma_\mu q^\prime(k)\bar{q}^\prime(k)\gamma_\nu q^\prime(k^\prime)\bar{q}^\prime(k^\prime)\right]
\times tr\left[\gamma^\mu q(p)\bar{q}(p)\gamma^\nu q(p^\prime)\bar{q}(p^\prime)\right].$$
It is precisely the mathematics by which the spinors lose their colour indices in-between these steps, that interests me!

Now, if I take the matrix element from above and introduce said new set of colour indices after squaring the matrix element, I get this result:
$$
|\mathcal{M}|^2=\frac{g^4}{t^2}\times t^a_{ij}t^{a\dagger}_{mn}t^b_{kl}t^{b\dagger}_{op}
\times tr\left[\gamma_\mu q^\prime_j(k)\bar{q}^\prime_n(k)\gamma_\nu q^\prime_i(k^\prime)\bar{q}^\prime_m(k^\prime)\right]
\times tr\left[\gamma^\mu q_l(p)\bar{q}_p(p)\gamma^\nu q_k(p^\prime)\bar{q}_o(p^\prime)\right].$$

So, how do I get from there to the textbook result above? I see that somehow we must get factors like $\delta_{im},\delta_{jn},\delta_{ko},\delta_{lp}$, such that
$$\delta_{im}\delta_{jn}\delta_{ko}\delta_{lp}t^a_{ij}t^{a\dagger}_{mn}t^b_{kl}t^{b\dagger}_{op}
=t^a_{ij}t^{a\dagger}_{ij}t^b_{kl}t^{b\dagger}_{kl}
=t^a_{ij}t^{a\ast}_{ji}t^b_{kl}t^{b\ast}_{lk}\\
=tr[t^at^{a\ast}]tr[t^bt^{b\ast}]
=C^2_F(N^2-1)^2.$$

 

[AndyW]

Thank you for your question. The issue with the colour indices in QCD calculations is a common confusion for many scientists. Let me try to explain it in a simple and intuitive way.

First of all, it is important to understand that the colour indices are a way to keep track of the different colour charges of the quarks involved in the process. In QCD, quarks carry a colour charge, which can be red, green or blue. Anti-quarks carry the corresponding anti-colour charge, i.e. anti-red, anti-green or anti-blue. Gluons, on the other hand, carry a combination of colour and anti-colour charges.

Now, when we calculate the matrix element for a process involving quarks and gluons, as in the example you provided, we are essentially dealing with a sum over all possible colour charges of the quarks and gluons. This is why we have the colour indices in the first place - to keep track of this sum.

However, when we square the matrix element, we are not only summing over the colour charges of the initial and final states, but also over the intermediate states. This is where the confusion usually arises. In the intermediate states, the quarks and gluons can be in any possible combination of colour charges, and this is why we have the delta functions, as you correctly pointed out in your calculations.

To put it simply, the delta functions ensure that we are summing over all possible colour charges in the intermediate states, and this is how we end up with the textbook result of $C^2_F(N^2-1)^2$. The spinors, on the other hand, do not carry a colour charge, so they do not have any colour indices. This is why they lose their colour indices in the squared matrix element.

I hope this explanation helps to clarify the issue. Keep up the good work with your calculations!