- #1
Ben_Walker1978
- 113
- 6
Homework Statement
[/B]
Hello, am i on the right track with this problem. I am not sure if i have done the it correct. The part i am unsure on is b). Not sure if i have calculated it correct.
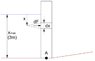
Part of a sea defence consists of a section of a concrete wall 4 metres high, and 6 metres wide. (See cross-section of the wall in the figure below).
a) Calculate the resultant thrust on the section when the sea reaches a height of 3 metres relative to the base of the section.
b) Calculate the overturning moment experienced by the section about point A.
Homework Equations
The Attempt at a Solution
Attachments
Last edited: