- #1
babu9000
I have a rigid body pendulum that is used to strike an object at the bottom of its swing. Ultimately I would like to know how much forced is the object being struck with. Could I do this with just knowing the velocity of the weight? I was thinking then I could get P=MV. Can someone please help e figure this out. Please see the attached diagrams.
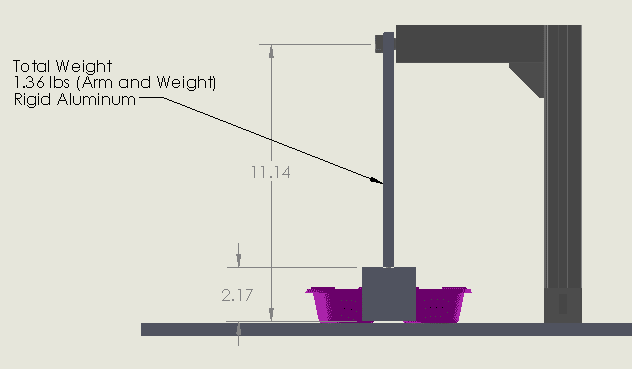
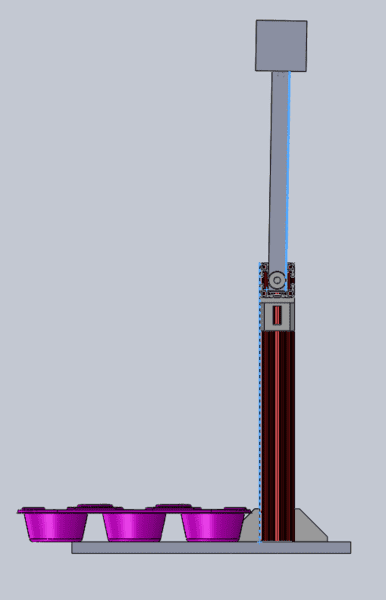
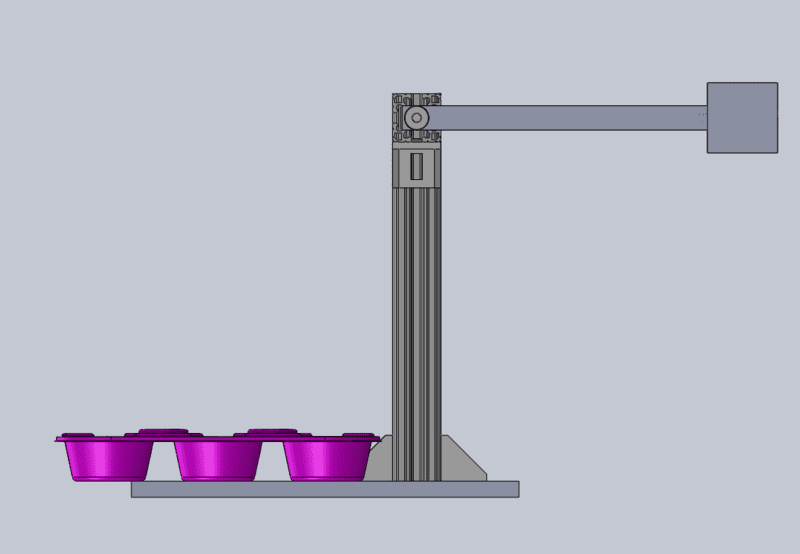

Last edited by a moderator: