- #1
Kolika28
- 146
- 28
Homework Statement
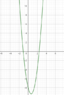
You are given the function
f(x)=3x^2-4x-8
a) Find the values of a.
Explain the answers using the function.
Homework Equations
The Attempt at a Solution
a^3-2*a^2-8*a=0
a=-2 v a=0 v a=4
I found the answers, but I don't know how to explain my answers by using the function. What does the zeros of the orginal function has to do with the function I integrated?
Thank you so much for help
Attachments
Last edited: