- #1
mr_k
- 9
- 0
hi!
i need help with problem:
Let F(u,v) be the Fourier transform of an M x N image f(x,y). Let g(x,y) be an image of dimensions (2 M) x (2 N) whose Fourier transform G(u,v) is defined as follows:
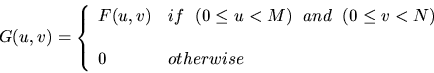
What does the image g(x,y) look like in terms of f(x,y)?
my solution : g(x,y)=0.25f(x/2,y/2).
Is that true?
thanks :)
i need help with problem:
Let F(u,v) be the Fourier transform of an M x N image f(x,y). Let g(x,y) be an image of dimensions (2 M) x (2 N) whose Fourier transform G(u,v) is defined as follows:
What does the image g(x,y) look like in terms of f(x,y)?
my solution : g(x,y)=0.25f(x/2,y/2).
Is that true?
thanks :)