- #1
PaintballerCA
- 25
- 0
Question:
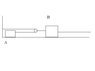
In the figure below, block B is moving with a speed of 3 ft/s at t=0. Block A has a weight of 10 lb and B has a weight of 3 lb. If the surface A is on is smooth, what is the velocity of A at t=1?
Attempt:
Given the pully set-up, V(A) should be twice that of V(B) since for any distance travled by B will require twice that distance in rope. So, 2V(B) = V(A). My other equation is the principle equation of impluse and momentum:
M(1)V(1) + integral(F*dt) = M(2)V(2)
For this problem, that gives:
[M(A)V(A1) + M(B)V(B1)] + integral(F*dt) = [M(A)V(A2) + M(B)V(B2)]
2V(B) = V(A)
For this problem, the force acting on the system is that of gravity on block B, so integral(F*dt) is a constant force integrated over the change in time (1 second), for an impluse of 3 lb*s.
Problem:
When I do this, I get a final velocity of 14.8 ft/s for block A, which is wrong (block A should have a velocity of 10.5 ft/s after 1 second) and I am not sure where I am making a mistake.
In the figure below, block B is moving with a speed of 3 ft/s at t=0. Block A has a weight of 10 lb and B has a weight of 3 lb. If the surface A is on is smooth, what is the velocity of A at t=1?
Attempt:
Given the pully set-up, V(A) should be twice that of V(B) since for any distance travled by B will require twice that distance in rope. So, 2V(B) = V(A). My other equation is the principle equation of impluse and momentum:
M(1)V(1) + integral(F*dt) = M(2)V(2)
For this problem, that gives:
[M(A)V(A1) + M(B)V(B1)] + integral(F*dt) = [M(A)V(A2) + M(B)V(B2)]
2V(B) = V(A)
For this problem, the force acting on the system is that of gravity on block B, so integral(F*dt) is a constant force integrated over the change in time (1 second), for an impluse of 3 lb*s.
Problem:
When I do this, I get a final velocity of 14.8 ft/s for block A, which is wrong (block A should have a velocity of 10.5 ft/s after 1 second) and I am not sure where I am making a mistake.