- #1
Warr
- 120
- 0
Hi
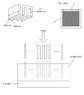
I have a problem I'm trying to figure out, but no idea where to start. Essentially I am trying to calculate the amount of force required to imprint 'photoresist' (a very viscous fluid sensitive to light) of some known density, [tex]\rho[/tex] and viscosity, [tex]\mu[/tex], with a ridid stamp, given a certain amount of time, t, and a certain depth, d.
Since I've never taken a fluid dynamics course, and am not sure if concepts from basic fluid dynamics are even relevant at these scales (lets say the stamp features are just an array of walls 100 nm wide and 1 micron depth, resembling a stripe pattern).
Is it harder to break through the surface of the fluid? Will the sides of the stamp 'walls' cause extra (non-negligable) resistance as opposed to a stamp with just a single feature (lets say a square) with the same surface area of all the walls in the first stamp? Is there a difference whether or not this is done in vacuum?
I've also attached a picture I created to help visualize the situation. Thank you for any help you can provide.
I have a problem I'm trying to figure out, but no idea where to start. Essentially I am trying to calculate the amount of force required to imprint 'photoresist' (a very viscous fluid sensitive to light) of some known density, [tex]\rho[/tex] and viscosity, [tex]\mu[/tex], with a ridid stamp, given a certain amount of time, t, and a certain depth, d.
Since I've never taken a fluid dynamics course, and am not sure if concepts from basic fluid dynamics are even relevant at these scales (lets say the stamp features are just an array of walls 100 nm wide and 1 micron depth, resembling a stripe pattern).
Is it harder to break through the surface of the fluid? Will the sides of the stamp 'walls' cause extra (non-negligable) resistance as opposed to a stamp with just a single feature (lets say a square) with the same surface area of all the walls in the first stamp? Is there a difference whether or not this is done in vacuum?
I've also attached a picture I created to help visualize the situation. Thank you for any help you can provide.