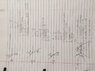Index of Refraction in prism

[Fan]

Homework Statement

A ray of light passes through a prism, making the minimum angle of deviation. The rays enter and emerge at 37degree from the normal to the surface. What is the index of refraction of the material, if the prism angle is 50degree?[/B]

Homework Equations

[PLAIN]http://www.eserc.stonybrook.edu/projectjava/snell/image39L.jpg [Broken] [Broken]

The Attempt at a Solution

[PLAIN]http://www.eserc.stonybrook.edu/projectjava/snell/image39L.jpg [Broken] [Broken]
(1.0)Sin(37)=1.33(Sin_2) = 0.45 with an angle of 27 degree

I know i need to solve for one of the "N" . I am confused as to which N do i solve for and do i still use the standard of 1 and 1.33 for N?

I have no idea how to rotate the image so i apologize in advance for the neck breaker.

Thank you for your help

 

[gneill]

It's convenient to take the external quantities n₁ and θ₁ to be the conditions where the light is entering the prism. So n₁ would be the index of refraction of air in this case.

The index of refraction of the prism material is an unknown at this point, and it's what you are meant to solve for. Looks like you'll need to determine the angle of refraction θ₂ in order to employ your Snell's Law equation. What other information is in the problem statement that might allow you to do that?