Index of refraction Thin Films

[blue_lilly]

Homework Statement

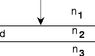
The diagram shows light incident from above on a film of thickness d. Each of the three materials in the figure can be chosen to be air, with index of refraction n=1.00, water, with index n=1.33, or glass, with index n=1.50. Under which of the following conditions will the reflected light be completely or nearly eliminated by interference?
(lambda2 refers to the wavelength of the light inside the thin film.)
(Note: In the case that d<<lambda2, you can assume the thickness is so small that the travel distance in material 2 has negligible affect on the phase of the wave. Treat this as if the two interfaces are almost right on top of each other.)
http://s3.amazonaws.com/answer-board-image/390a9f5e-a2a9-4fbe-a6f6-c33689d8251c.gif

1) T/F d=lambda2/4, material 1 is air, 2 is water, 3 is glass.
2) T/F d=lambda2/2, material 1 is air, 2 is water, 3 is glass.
3) T/F d=lambda2/4, material 1 is glass, 2 is air, 3 is glass.
4) T/F d=lambda2/4, material 1 is water, 2 is glass, 3 is air.
5) T/F d<<lambda2, material 1 is water, 2 is glass, 3 is air.

Homework Equations

2*n*d*sinθ = (m-(1/2))*λ

m=integer
λ=wavelength
n=index of refraction = speed of light in vacuum/speed of light in medium
d= thickness
​

The Attempt at a Solution

We are looking for places where the refracted light is eliminated by interference, so we are looking for destructive interference.
Destructive if Path-length Difference(PLD) 2nd= (m + (1/2))λ when the sources are exactly in phase.
Destructive if Path-length Difference(PLD) 2nd = mλ when the sources are exactly out of phase.
There are phase reversals when it is reflecting of a higher n.

1) d=lambda2/4, material 1 is air(n=1.00), 2 is water, 3 is glass.
True because

There would be 2 phase reversals [1 between air and water and the other between water and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ
d=2λ/4
(2λ/4) = (1/2)λ
(2/4)λ= (1/2)λ
(1/2)λ= (1/2)λ
​

2) d=lambda2/2, material 1 is air(n=1.00), 2 is water(n=1.33), 3 is glass(n=1.50).
False because

There would be 2 phase reversals [1 between air and water and the other between water and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ
d=2λ/2
2λ/2 = (1/2)λ
(2/2)λ = (1/2)λ​

3) d=lambda2/4, material 1 is glass(n=1.50), 2 is air(n=1.00), 3 is glass(n=1.50).
True because

There would be 2 phase reversals [1 between air and glass and the other between air and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ.
d=2λ/4
(2λ/4) = (1/2)λ
(2/4)λ= (1/2)λ
(1/2)λ= (1/2)λ
​

4) d=lambda2/4, material 1 is water(n=1.33), 2 is glass(n=1.50), 3 is air(n=1.00).
True because

There would be 2 phase reversals [1 between air and water and the other between the water and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ.
d=2λ/4
(2λ/4) = (1/2)λ
(2/4)λ= (1/2)λ
(1/2)λ= (1/2)λ
​

5) d<<lambda2, material 1 is water(n=1.33), 2 is glass(n=1.50), 3 is air(n=1.00).
False because

There would be 2 phase reversals [1 between air and water and the other between the water and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ.
d<<lambda2
λ2= (1/2)λ
​

I thought i was doing right but the answer is incorrect.
Any help would be greatly appreciated.

 

[TSny]

Hello.

You are not getting the number of phase reversals correct for some of the cases. How do you decide if a phase reversal occurs?

 

[blue_lilly]

Hello.

You are not getting the number of phase reversals correct for some of the cases. How do you decide if a phase reversal occurs?

A phase reversal happens when the n it is "hitting" is larger then what the "n" was before.

1) d=lambda2/4, material 1 is air(n=1.00), 2 is water(n=1.3), 3 is glass(n=1.5).
So for this one the wave is traveling in air and then it hits water, which has a higher "n" value. this means that part of the wave is reflected back and part continues through the water. The wave traveling in the water "hits" the glass and glass has a higher "n" value then water so part of the wave reflects back and some continues through the object.

I thought this was how you are supposed to tell. Is it incorrect?

 

[TSny]

Yes. You got this one right. But some of the other cases are incorrect. For example, check case(3).

 

[HalfLostAndSearching]

Your attempt at a solution is on the right track, but there are a few errors in your reasoning. First, let's clarify some concepts:

1. Path-length difference (PLD) refers to the difference in distance traveled by two waves. This can be calculated by taking the difference in the path lengths of the two waves, which is equal to the thickness of the film (d). This is important because the PLD determines whether the waves are in or out of phase and therefore whether we have constructive or destructive interference.

2. Phase refers to the position of a wave in its cycle. When two waves are in phase, their crests and troughs line up and they reinforce each other. When they are out of phase, their crests and troughs are misaligned and they cancel each other out.

Now, let's go through each statement and see where things went wrong:

1) T/F d=lambda2/4, material 1 is air(n=1.00), 2 is water, 3 is glass.
True because
There would be 2 phase reversals [1 between air and water and the other between water and glass] So the wavelength would be exactly in phase which means it needs to have PLD of (1/2)λ
d=2λ/4
(2λ/4) = (1/2)λ
(2/4)λ= (1/2)λ
(1/2)λ= (1/2)λ

Your reasoning here is mostly correct, but there are a few small errors. First, the PLD for destructive interference is (1/2)λ, not (1/4)λ. This means that the thickness of the film (d) should be equal to (1/2)λ, not (1/4)λ. So the correct statement would be "d=lambda2/2". Also, your calculation of d=2λ/4 is incorrect. It should be d=(1/2)λ. Finally, your last line "(1/2)λ= (1/2)λ" is unnecessary and doesn't add any new information.

2) T/F d=lambda2/2, material 1 is air(n=1.00), 2 is water(n=1.33), 3 is glass(n=1.50).
False because
There would be 2 phase reversals [1 between air