- #1
NaOH
- 31
- 0
Homework Statement
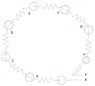
It is often discussed that a changing magnetic field will create a non-conservative electric field, which would then induces an EMF and hence an induced current, but what happens when we connect voltmeters?
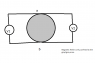
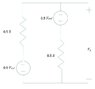
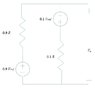
Consider putting a circular loop of wire with some resistance in a changing magnetic field. The magnetic field can be said to only affect the loop. Now I attach an ideal voltmeter to 2 points on the loop, what would be observed on the voltmeter?
Homework Equations
Faraday's law, E = change in flux wrt time
The Attempt at a Solution
This is qualitative, so not much. There could be a few cases.
One: I just get the full EMF value.
Two: I get a fraction of the full EMF value proportional to arc length tapped. Runs into problem when I consider what the positive sense of the potential is when it is tapped at the diameter of the loop.
Three: 0. Either because EMF is the same at any point, or that whatever EMF the arc length subtended is consumed by the current and resistance of the subtended arc.
Four: not useful to define potential difference because electric field is not conserved. it does not explain how the voltmeter will respond.