Induced magnetic field loophole?

[athrun200]

Homework Statement

The problem I would like to ask is in Griffiths Introduction to Electrodynamics p358 problem 8.6 part (c)

Homework Equations

The Attempt at a Solution

The answer is $${\varepsilon _0}EBAd\hat y$$ which is same as part (a)
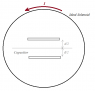
Here's how I found a loophole:One key information that will come in handy later is: the magnetic field is now decreasing, which will produce a electric field.

Before finding the impulse, we need to find the force acting on the capacitor since
$$\overrightarrow I = \int {\overrightarrow F \cdot dt} $$
The force, which is caused by the induced electric field, is simply
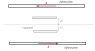
$$\overrightarrow F = \sigma A[ - E(d) + E(0)]\widehat y$$
To eliminate the induced electric field, I use the following equation
$$\oint {\vec E \cdot d\vec l} = \int\limits_S {\vec \nabla \times \vec E \cdot d\vec a = - ld{{\partial \vec B} \over {\partial t}}} $$
Now consider only the line integral on the left hand side
$$\oint {\vec E \cdot d\vec l} = \int\limits_l^0 {E(d)dx + } \int\limits_d^0 {{E_1}dy + } \int\limits_0^l {E(0)dx + } \int\limits_0^d {{E_2}dl} $$
$$ = l[ - E(d) + E(0)] + d({E_2} - {E_1})$$
Here's the problem. Useless $${E_2} - {E_1} = 0$$
,otherwise there is no way to find $$ - E(d) + E(0)$$
However $${E_2} - {E_1} = 0$$ implies $${E_2} = {E_1}$$
this symmetry would cause $$ E(d) = E(0)$$ otherwise it is really awkward.

What's wrong?

 

[TSny]

I'm a little confused with how your axes are oriented. According to your calculations, B is the z direction. But you also state that the answer for the electromagnetic momentum is in the z direction. This can't be right, as the momentum must be perpendicular to B.

(In my copy of Griffiths (3rd edition) the plates are perpendicular to the z axis and B is in the x direction.)

But, anyway, I think you have a good question. If the magnetic field $\vec{B}(t)$ is uniform throughout all of infinite 3D space, then there is an ambiguity in the direction of the induced electric field caused by the changing magnitude of the B field. Every point of the infinite space should be equivalent in regards to the magnetic field and the corresponding induced E-field. So, if the induced electric field points in some direction at one point of space, it would seem that the induced E-field should point in the same direction with the same magnitude at every other point of space. But that would contradict Maxwell's equation $\vec{\nabla} \times \vec{E} = -\frac{\partial{\vec{B}}}{\partial t}$.

So, I think you need to assume that the B field does not really extend to infinity in all directions. For example, you could take the B field as being produced by two infinite parallel plates oriented parallel to the capacitor plates as shown in the figure below. Each infinite plate carries a uniform current density J so as to produce a uniform B field out of the page between the infinite plates. The capacitor is placed symmetrically between the infinite plates. B is decreased by letting J decrease. For this geometry, you should be able to deduce the direction of the induced E field. Try to show that the direction of the induced E-field is parallel to the plates. There is no component of induced E field perpendicular to the capacitor plates.

Or, you could use a large, ideal solenoid to produce the B field out of the page. See the other figure. B is decreased by letting the current I in the solenoid decrease. You should now be able to show that the induced E-field lines are circular. You can work out the force on the capacitor plates due to this induced E-field and show that you get the same result for the force as for the infinite plates configuration.

 

[athrun200]

Thanks. I fixed the confusion of the coordinates

For the infinite plate, I can deduce the direction of induced electric field by using right hand rule.

But I have some problem in finding induced electric field by using mathematical method.

I used this equation to find the induced electric field.
$$\vec \nabla \times \vec E = - {{\partial \vec B} \over {\partial t}}$$

Since magnetic field is along x-axis and it is decreasing,
$${{\partial \vec B} \over {\partial t}} = ( - \alpha ,0,0) $$ where $$\alpha$$ is a constant

Now, I express the curl on the left hand side into matrix,
$$\left| {\matrix{
{\hat x} & {\hat y} & {\hat z} \cr
{{\partial \over {\partial x}}} & {{\partial \over {\partial y}}} & {{\partial \over {\partial z}}} \cr
{{E_x}} & {{E_y}} & {{E_z}} \cr

} } \right|$$

by equating the left and the right, I generated 3 differntial equations
$$\eqalign{
& {{\partial {E_x}} \over {\partial z}} = {{\partial {E_z}} \over {\partial x}} \cr
& {{\partial Ey} \over {\partial x}} = {{\partial {E_x}} \over {\partial y}} \cr
& {{\partial {E_z}} \over {\partial y}} - {{\partial {E_y}} \over {\partial z}} = \alpha \cr} $$

It seems they are unsolvable
Before I proceed, I would like to know if this method is correct.

 

[TSny]

To obtain specific solutions to the differential equations, you have to impose additional constraints on the fields such as boundary conditions or other conditions associated with the geometry.

For example, consider the case I gave earlier where the B field is produced by two current-carrying, infinite plates oriented parallel to the xy plane. The B field is invariant under any translations parallel to the xy plane. So, it seems to me that the induced E field produced by changing the magnitude of B would also have to be invariant under translations parallel to the xy plane. That is, the induced electric field cannot depend on x or y. So each component of E is a function of z only. (This argument might be too hand-wavy. Hopefully, someone will point out if its wrong or if there is a more rigorous argument.)

So, if you accept that the components of E are functions of z alone, see what you can deduce from your differential equations. You might also want to see if $\vec{\nabla}\cdot\vec{E} = 0$ give you any information.

 

[TSny]

The problem I would like to ask is in Griffiths Introduction to Electrodynamics p358 problem 8.6 part (c)

The answer is $${\varepsilon _0}EBAd\hat y$$ which is same as part (a)

Apparently this answer of Griffiths is incorrect, as Griffiths himself points out in a paper in the American Journal of Physics:

"Hidden momentum, field momentum, and electromagnetic impulse" by
David Babson, Stephen P. Reynolds, Robin Bjorkquist and David J. Griffiths
Am. J. Phys. 77, 826 (2009)

According to this paper, the answers to parts (a) and (c) are $\frac{1}{2}{\varepsilon _0}EBAd\hat y$, or half the value given above.

The correction of 1/2 for part (a) is due to the need to include the fringing of the electric field of the capacitor. (It's surprising that the fringing accounts for a 50% reduction in the momentum stored in the fields.)

There are various subtleties to this problem that are discussed in this paper.