- #1
fayled
- 177
- 0
Homework Statement
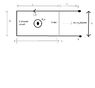
An induction device is set up as shown below. It has a U-shaped conductor of negligible resistance along which a conducting slider of resistance R moves in the x direction. The assembly is immersed in a uniform magnetic flux density B of magnitude B0 that is directed out of the page. The slider is moved such that its position with respect to the end of the U-shaped conductor is given by x=L+x0coswt with x0<L.
I need to derive the voltage across AB and the current flowing around the U.
Then I need to find the voltage across AB when the U has a resistance per unit length alpha.
Homework Equations
Faraday's law. V=IR.
The Attempt at a Solution
The induced emf is B0dx0wsinwt in both cases. This is induced in the sliding rod.
Now comes my confusion.
In the first case, I believe we have a voltage rise across the rod, and a voltage drop of equal magnitude across the rod due to the resistance. These cancel so V=0. The current that flows is B0lx0wsinwt/R.
In the second case, we now have a voltage rise across the rod, some voltage drop due to a resistance R, and then around the U conductor a voltage drop due to a resistance of R'=α[d+2(L+x0coswt)]. Thus I believe the voltage drop across A and B should be the induced emf minus the the circuit current times the resistance R, with the circuit current the induced emf over total resistance. However the answer is in fact only the second component, i.e just the current times R.
Thanks for any help in advance.