- #1
Onezimo Cardoso
Homework Statement
Homework Equations
The Attempt at a Solution
[/B]
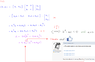
I could show that the first of the three properties are valid for any value of a,b,c but I couldn’t find a way to show the forth one.
Follow all the procedures I already did: