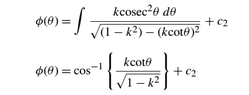Solving Integral in Picture: Step-by-Step Guide

[FilipVz]

View attachment 1922

Can somebody explain how to solve integral from the picture above?( solution is in the second line)

 

[Jameson]

I haven't worked out the solution yet, but given the answer and the general form of the integral I would guess trig substitution is the way to solve it. Question though - should the $(1-k^2)$ in the denominator actually be $(1-k^2)^2$?

If that's not the way to solve it then maybe there's something with the substitution $(k \cot(\theta))^2=k^2 \cot^2(\theta)=k^2(\csc^2(\theta)-1)$, but I'm not sure yet. Will post back if anything comes to mind.

 

[alyafey22]

Hint :

\(\displaystyle \frac{d}{dx} \left(\cos^{-1} (f) \right) = \frac{-f'}{\sqrt{1-f^2}}\)​

 

[MarkFL]

Hint: Try the substitution:

\(\displaystyle \cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)\)

Hence:

\(\displaystyle \csc^2(\theta)\,d\theta=\frac{\sqrt{1-k^2}}{k}\sin(u)\,du\)

And the result will follow. :D

 

[alyafey22]

Hint: Try the substitution:

\(\displaystyle \cot(\theta)=\frac{\sqrt{1-k^2}}{k}\cos(u)\)

Hence:

\(\displaystyle \csc^2(\theta)\,d\theta=\frac{\sqrt{1-k^2}}{k}\sin(u)\,du\)

And the result will follow. :D

No need for substitution. Of course it is more advisable on an elementary level .

 

[FilipVz]

Thank you,

i solved it, using substitution:

\(\displaystyle u= (k*ctgθ)/(1-k^2 )\)

But, my result is:

\(\displaystyle ϕ=-arcsin((k∙ctgθ)/√(1-k^2 ))+c_2\)

instead of

\(\displaystyle ϕ=arccos((k∙ctgθ)/√(1-k^2 ))+c_2\)

Is this correct?

 

[MarkFL]

Thank you,

i solved it, using substitution:

\(\displaystyle u= (k*ctgθ)/(1-k^2 )\)

But, my result is:

\(\displaystyle ϕ=-arcsin((k∙ctgθ)/√(1-k^2 ))+c_2\)

instead of

\(\displaystyle ϕ=arccos((k∙ctgθ)/√(1-k^2 ))+c_2\)

Is this correct?

Yes, that's another possible form. Consider the identity:

\(\displaystyle \sin^{-1}(x)+\cos^{-1}(x)=\frac{\pi}{2}\)

along with the fact that the sum of an arbitrary constant and another constant is still an arbitrary constant. :D

 

[alyafey22]

\(\displaystyle \int \frac{-1}{\sqrt{1-x^2}} \, dx = \cos^{-1}(x)+A\)

\(\displaystyle -\int \frac{1}{\sqrt{1-x^2}} \, dx = -\sin^{-1}(x)+B\)

And this simply because

\(\displaystyle \cos^{-1}(x)+\sin^{-1}(x) =\frac{\pi}{2}\)